
����Ŀ������������Ҫ����Ⱦ���ŷ�����������ɢ�����ص�Ӱ�죬ij�л������վ2014��10������10�죨�����Ҷ�Ӧ1����10�ţ��ɼ�����ij��ƽ�����ټ���������������վ�Ũ�����ݣ��Ƴ�ɢ��ͼ��ͼ��ʾ��
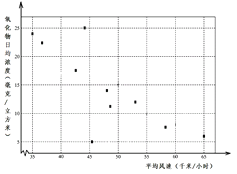
����ͬѧ�״���10���������ȡ����5����һ�����ݣ�����ع�ֱ�߷��̣���������5����һ��������ǡ��ͬʱ�����������վ�Ũ���������Сֵ�ĸ��ʣ�
��������30��ѧ����ÿ����ȡ5�����ݣ���Ӧ�����30����ͬ�Ļع�ֱ�߷��̣���֪30���������а����������վ�Ũ����ֵ����14�飮�ֲ�����30���ع鷽�̶�ijһ��ƽ�������µ��������վ�Ũ�Ƚ���Ԥ�⣬��Ԥ��ֵ��ʵ��ֵ��ľ���ֵС��2�����֮Ϊ�����Ч���á�������Ϊ�����Ч�����á�������������Ϣ�������2��2�������������Ƿ���95%���ϵİ���˵���Ч����ѡȡ�����Ƿ�����������վ�Ũ����ֵ�йأ�
Ԥ��Ч���� | ���Ч������ | �ϼ� | |
�����а�����ֵ | 5 | ||
�����ް�����ֵ | 4 | ||
�ϼ� |
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
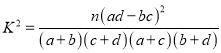 ������
������![]() ��.
��.
���𰸡���1��![]() ��2����95%���ϵİ���
��2����95%���ϵİ���
�������������������1������ö�ٷ�ȷ������10���������ȡһ������5������ݰ����Ļ����¼�����6��������ȷ����������ǡ��ͬʱ�����������վ�Ũ���������Сֵ�������Ļ����¼���4�����������ݹŵ�����ʹ�ʽ����ʣ�2���ȸ���ɢ��ͼ����д��Ӧ���ݣ��ٸ��ݹ�ʽ��![]() ���ٶ��ղο����ݣ�ȷ�������Զ��.
���ٶ��ղο����ݣ�ȷ�������Զ��.
������������ǵ�![]() ��������Ϊ
��������Ϊ![]() ��
��![]() ������ͼ����֪
������ͼ����֪![]() ���վ�Ũ�����
���վ�Ũ����� ![]() ���վ�Ũ����С������10���������ȡһ������5������ݰ����Ļ����¼��У�
���վ�Ũ����С������10���������ȡһ������5������ݰ����Ļ����¼��У� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����6�֣�
����6�֣�
���¼�![]() ��������ǡ��ͬʱ�����������վ�Ũ���������Сֵ�������Ļ����¼��У�
��������ǡ��ͬʱ�����������վ�Ũ���������Сֵ�������Ļ����¼��У� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����4�֣�
����4�֣�
������5���������ǡ��ͬʱ�����������վ�Ũ����ֵ�ĸ���![]() ��
��
���������⣬���2��2����������ʾ��
Ԥ��ȷ | Ԥ�ⲻȷ | �ϼ� | |
�����а�����ֵ | 5 | 10 | 15 |
����û�а�����ֵ | 11 | 4 | 15 |
�ϼ� | 16 | 14 | 30 |
�ɹ�ʽ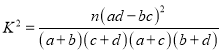 �������
�������![]() ��
��
�ɲο����ݿ�֪�� ![]() ������95%���ϵİ���˵���Ч����ѡȡ�����Ƿ�����������վ�Ũ����ֵ�йأ�
������95%���ϵİ���˵���Ч����ѡȡ�����Ƿ�����������վ�Ũ����ֵ�йأ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��麯������ͬһֱ������ϵ��f��x����g��x����ͬ��һ���ǣ� ��
A.f��x��= ![]() ��g��x��=
��g��x��= ![]()
B.f��x��= ![]() ��g��x��=x��3
��g��x��=x��3
C.f��x��= ![]() ��g��x��=
��g��x��= ![]()
D.f��x��=x��g��x��=lg��10x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f(x)��![]() (a>0��a��1)�Ƕ�����ΪR���溯����
(a>0��a��1)�Ƕ�����ΪR���溯����
������f(1)>0������ʽf(x2��2x)��f(x��4)>0�Ľ⼯��
������f(1)��![]() ����g(x)��a2x��a��2x��4f(x)����g(x)��[1������)�ϵ���Сֵ��
����g(x)��a2x��a��2x��4f(x)����g(x)��[1������)�ϵ���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѻ���y=cos2x+ ![]() sin2x��ͼ������ƽ��m������m��0������λ������ͼ�����y��Գƣ���m����Сֵ�ǣ� ��
sin2x��ͼ������ƽ��m������m��0������λ������ͼ�����y��Գƣ���m����Сֵ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݡ������������500ǧ�ף�һ������������������ʻ�����ݣ��涨�ٶȲ��ó���100ǧ��/Сʱ����֪����ÿСʱ������ɱ�����ԪΪ��λ���ɿɱ䲿�̶ֺ�������ɣ��ɱ䲿�����ٶ�v��ǧ��/ʱ����ƽ�������ȣ�����ϵ��Ϊ0.01���̶�����ΪaԪ��a��0����
��1����ȫ������ɱ�y��Ԫ����ʾΪ�ٶ�v��ǧ��/ʱ���ĺ�������ָ����������Ķ�����
��2��Ϊ��ʹȫ������ɱ���С������Ӧ�Զ���ٶ���ʻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ��ȷ���Ķ���Ǧ���l���£�a��b�ǿռ����������ֱ�ߣ�������������ĸ������У���ʹa��b���ɵĽ�Ҳȷ�����ǣ� ��
A.a��a��b��
B.a��a��b�ͦ�
C.a����b�ͦ�
D.a�ͦ���b�ͦ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�ĸ����Ϊ��������ǰn��ĺ�ΪSn���Ҷ������m��n��N*��
����(Sm��n��S1)2��4a2ma2n��
��1����![]() ��ֵ��
��ֵ��
��2����֤��{an}Ϊ�ȱ����У�
��3����֪����{cn}��{dn}����|cn|��|dn|��an��p(p��3)�Ǹ�����������������{cn}��{dn}��ǰp��ĺͷֱ�ΪTp��Rp����Tp��Rp����֤��������������k(1��k��p)��ck��dk��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������7ʱ�˴�������������![]() ����/Сʱ
����/Сʱ![]() ��
��![]() ��ǰ�����50�����
��ǰ�����50�����![]() �ۣ�Ȼ�������������
�ۣ�Ȼ�������������![]() ǧ��/Сʱ(
ǧ��/Сʱ(![]() )��
)��![]() ��ǰ�����
��ǰ�����![]() ǧ��
ǧ��![]() �У��ƻ���������4��9ʱ����
�У��ƻ���������4��9ʱ����![]() ��.��˴�����������Ҫ��ʱ��ֱ�Ϊ
��.��˴�����������Ҫ��ʱ��ֱ�Ϊ![]() ��
��![]() Сʱ���������Ҫ�ľ���
Сʱ���������Ҫ�ľ���![]() (��λ��Ԫ)
(��λ��Ԫ)

(1)���ú���![]() ��
��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��
(2)Ҫʹ�����辭��![]() ���٣���
���٣���![]() ��
��![]() ��ֵ���������ʱ�ķ���.
��ֵ���������ʱ�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣨0��4����б��Ϊ��1��ֱ����������y2=2px��p��0����������A��B������|AB|�ij���Ϊ4![]() ��
��
��1����p��ֵ��
��2����֤��OA��OB��OΪԭ�㣩��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com