
【题目】(本题满分12分)已知椭圆![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(Ⅱ)若![]() 过点
过点![]() ,延长线段
,延长线段![]() 与
与![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求此时
能否为平行四边形?若能,求此时![]() 的斜率,若不能,说明理由.
的斜率,若不能,说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)能,![]() 或
或![]() .
.
【解析】
试题分析:(1)设直线![]()
![]() ,直线方程与椭圆方程联立,根据韦达定理求根与系数的关系,并表示直线
,直线方程与椭圆方程联立,根据韦达定理求根与系数的关系,并表示直线![]() 的斜率,再表示
的斜率,再表示![]() ;
;
(2)第一步由 (Ⅰ)得![]() 的方程为
的方程为![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,直线
,直线![]() 与椭圆方程联立求点
与椭圆方程联立求点![]() 的坐标,第二步再整理点
的坐标,第二步再整理点![]() 的坐标,如果能构成平行四边形,只需
的坐标,如果能构成平行四边形,只需![]() ,如果有
,如果有![]() 值,并且满足
值,并且满足![]() ,
,![]() 的条件就说明存在,否则不存在.
的条件就说明存在,否则不存在.
试题解析:解:(1)设直线![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴由![]() 得
得![]() ,
,
∴![]() ,
,![]() .
.
∴直线![]() 的斜率
的斜率![]() ,即
,即![]() .
.
即直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值
的斜率的乘积为定值![]() .
.
(2)四边形![]() 能为平行四边形.
能为平行四边形.
∵直线![]() 过点
过点![]() ,∴
,∴![]() 不过原点且与
不过原点且与![]() 有两个交点的充要条件是
有两个交点的充要条件是![]() ,
,![]()
由 (Ⅰ)得![]() 的方程为
的方程为![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
∴由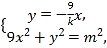 得
得![]() ,即
,即![]()
将点![]() 的坐标代入直线
的坐标代入直线![]() 的方程得
的方程得![]() ,因此
,因此![]() .
.
四边形![]() 为平行四边形当且仅当线段
为平行四边形当且仅当线段![]() 与线段
与线段![]() 互相平分,即
互相平分,即![]()
∴![]()
![]() .解得
.解得![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴当![]() 的斜率为
的斜率为![]() 或
或![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销量y(元) | 88 | 78 | 85 | 75 | 82 | 66 |
(1)分别以三家连锁店的平均售价与平均销量为散点,如A店对应的散点为![]() ,求出售价与销量的回归直线方程
,求出售价与销量的回归直线方程![]() ;
;
(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附: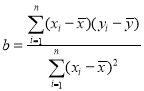 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 为“可等域函数”,区间
为“可等域函数”,区间![]() 为函数
为函数![]() 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
①![]() ;②
;②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
其中存在唯一“可等域区间”的“可等域函数”为( )
(A)①②③ (B)②③ (C)①③ (D)②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
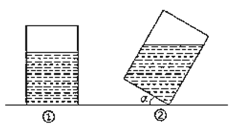
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
, ![]() ,点
,点![]() 满足:
满足: ![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
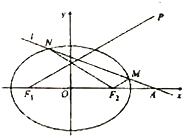
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若斜率为![]() (
(![]() )的直线
)的直线![]() 与
与![]() 轴、椭圆
轴、椭圆![]() 顺次相交于点
顺次相交于点![]() 、
、![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店 | A店 | B店 | C店 | |||
售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
销量y(元) | 88 | 78 | 85 | 75 | 82 | 66 |
(1)分别以三家连锁店的平均售价与平均销量为散点,如A店对应的散点为![]() ,求出售价与销量的回归直线方程
,求出售价与销量的回归直线方程![]() ;
;
(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附: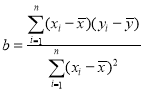 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试中,五名学生的数学、物理成绩如下表所示:
学生 | A1 | A2 | A3 | A4 | A5 |
数学(x分) | 89 | 91 | 93 | 95 | 97 |
物理(y分) | 87 | 89 | 89 | 92 | 93 |
(1)要从5名学生中选2人参加一项活动,求选中的学生中至少有一人的物理成绩高于90分的概率;
(2)请在所给的直角坐标系中画出它们的散点图,并求这些数据线性回归方程![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com