
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 与
与![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
【答案】(Ⅰ)椭圆![]() 的方程为
的方程为![]() , 点P的坐标为
, 点P的坐标为![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】分析:(I)由题意计算可得![]() ,
, ![]() , 则椭圆
, 则椭圆![]() 的方程为
的方程为![]() , 结合几何性质可得点P的坐标为
, 结合几何性质可得点P的坐标为![]() .
.
(II)由题意可知直线l2的斜率存在,设l2的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() , 由弦长公式可得
, 由弦长公式可得![]() ; 结合几何关系和勾股定理可得
; 结合几何关系和勾股定理可得![]() , 则面积函数
, 则面积函数![]() , 换元求解函数的值域可得△ABC的面积的取值范围是
, 换元求解函数的值域可得△ABC的面积的取值范围是![]() .
.
详解:(I)设![]() ,
,![]() ,
,
可知圆![]() 经过椭圆焦点和上下顶点,得
经过椭圆焦点和上下顶点,得![]() ,
,
由题意知![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ,
,
点P的坐标为![]() .
.
(II)由过点P的直线l2与椭圆![]() 相交于两点,知直线l2的斜率存在,
相交于两点,知直线l2的斜率存在,
设l2的方程为![]() ,由题意可知
,由题意可知![]() ,
,
联立椭圆方程,得![]() ,
,
设![]() ,则
,则![]() ,得
,得![]() ,
,
所以![]() ;
;
由直线l1与l2垂直,可设l1的方程为![]() ,即
,即![]()
圆心![]() 到l1的距离
到l1的距离![]() ,又圆的半径
,又圆的半径![]() ,
,
所以![]() ,
,
![]() ,
,
由![]() 即
即![]() ,得
,得![]() ,
,
![]()
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
当且仅当![]() 即
即![]() 时,取“=”,
时,取“=”,
所以△ABC的面积的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】
已知双曲线![]() 设过点
设过点![]() 的直线l的方向向量
的直线l的方向向量![]()
(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2) 证明:当![]() >
>![]() 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】p:关于x的方程![]() 无解,q:
无解,q:![]() (
(![]() )
)
(1)若![]() 时,“
时,“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数a的取值范围.
”为假命题,求实数a的取值范围.
(2)当命题“若p,则q”为真命题,“若q,则p”为假命题时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且点
两点,且点![]() 在第二象限.
在第二象限.![]() 与
与![]() 延长线交于点
延长线交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的3倍,求
面积的3倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国高铁的快速发展给群众出行带来巨大便利,极大促进了区域经济社会发展.已知某条高铁线路通车后,发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() ,经测算,高铁的载客量与发车时间间隔
,经测算,高铁的载客量与发车时间间隔![]() 相关:当
相关:当![]() 时高铁为满载状态,载客量为1000人;当
时高铁为满载状态,载客量为1000人;当![]() 时,载客量会在满载基础上减少,减少的人数与
时,载客量会在满载基础上减少,减少的人数与![]() 成正比,且发车时间间隔为5分钟时的载客量为100人.记发车间隔为
成正比,且发车时间间隔为5分钟时的载客量为100人.记发车间隔为![]() 分钟时,高铁载客量为
分钟时,高铁载客量为![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)若该线路发车时间间隔为![]() 分钟时的净收益
分钟时的净收益![]() (元),当发车时间间隔为多少时,单位时间的净收益
(元),当发车时间间隔为多少时,单位时间的净收益![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若等比数列![]() 的前n项和为
的前n项和为![]() ,求实数a的值;
,求实数a的值;
(2)对于非常数数列![]() 有下面的结论:若数列
有下面的结论:若数列![]() 为等比数列,则该数列的前n项和为
为等比数列,则该数列的前n项和为![]() (
(![]() 为常数).写出它的逆命题并判断真假,请说明理由;
为常数).写出它的逆命题并判断真假,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有![]() 的男生喜欢网络课程,有
的男生喜欢网络课程,有![]() 的女生不喜欢网络课程,且有
的女生不喜欢网络课程,且有![]() 的把握但没有
的把握但没有![]() 的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附: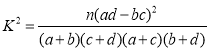 ,其中
,其中![]() .
.
|
|
|
|
|
k |
|
|
|
|
A.130B.190C.240D.250
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com