Question

已知数列1，2×3，3×3²，4×3³，…，n•3^n-1，…（n∈N^*），则其前n项的和S_n=    ．

Answer 1

【答案】分析：可得S_n=1+2×3+3×3²+4×3³+…+n•3^n-1 ①，两边同乘以3可得3S_n=1×3+2×3²+3×3³+4×3⁴+…+n•3ⁿ ②，①-②由错位相减法可得．
解答：解：由题意可得：
S_n=1+2×3+3×3²+4×3³+…+n•3^n-1 ①
两边同乘以3可得，
3S_n=1×3+2×3²+3×3³+4×3⁴+…+n•3ⁿ ②
①-②可得：
-2S_n=1+3+3²+3³+…+3^n-1-n•3ⁿ
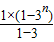
=-n•3ⁿ=，
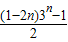
故S_n=，
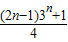
故答案为：
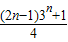点评：本题考查数列求和的错位相减法，属中档题．