
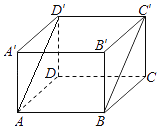
【题目】如图,长方体ABCD﹣A′B′C′D′中,AB=2 ![]() ,AD=2
,AD=2 ![]() ,AA′=2,
,AA′=2,
(Ⅰ)求异面直线BC′ 和AD所成的角;
(Ⅱ)求证:直线BC′∥平面ADD′A′.

【答案】(1) 异面直线BC′和AD所成的角为30°.
(2)证明见解析.
【解析】分析:(1)由AD∥BC,得∠CBC′是异面直线BC′和AD所成的角,由此能求出异面直线BC′和AD所成的角.(2)连结AD′,由AD′∥BC′,能证明直线BC′∥平面ADD′A′.
详解:(1)解:∵长方体ABCD﹣A′B′C′D′中,AD∥BC,∴∠CBC′是异面直线BC′和AD所成的角,
∵长方体ABCD﹣A′B′C′D′中,AB=2![]() ,AD=2
,AD=2 ![]() ,AA′=2,CC′⊥BC,
,AA′=2,CC′⊥BC,
∴tan∠CBC′=![]() ,
,
∴∠CBC′=30°,
∴异面直线BC′和AD所成的角为30°
(2)解:证明:连结AD′,
∵长方体ABCD﹣A′B′C′D′中,AD′∥BC′,
又AD′平面ADD′A′,BC′平面ADD′A′,
∴直线BC′∥平面ADD′A′


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】(题文)平面内动点![]() 到两定点
到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() ,则动点
,则动点![]() 的轨迹叫做阿波罗尼斯圆.现已知定点
的轨迹叫做阿波罗尼斯圆.现已知定点![]() 、
、![]() ,圆心为
,圆心为![]() ,
,
(1)求满足上述定义的圆![]() 的方程,并指出圆心
的方程,并指出圆心![]() 的坐标和半径;
的坐标和半径;
(2)若![]() ,且经过点
,且经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前北方空气污染越来越严重,某大学组织学生参加环保知识竞赛,从参加学生中抽取40名,将其成绩(均为整数)整理后画出的频率分布直方图如图,若从成绩是80分以上(包括80分)的学生中选两人,则他们在同一分数段的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过
经过![]() ,且椭圆
,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设斜率存在的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() ,且
,且![]() 与圆心为
与圆心为![]() 的定圆
的定圆![]() 相切.直线
相切.直线![]() :
:![]() (
(![]() )与圆
)与圆![]() 交于
交于![]() 两点,
两点,![]() .求
.求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,抛物线
,抛物线![]() 的焦点在
的焦点在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点,点
的顶点均为原点,点 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,
(1)求曲线![]() ,
, ![]() 的标准方程;
的标准方程;
(2)请问是否存在过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,使得以线段
,使得以线段![]() 为直径的圆过原点
为直径的圆过原点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com