解:(1)∵f(x)>a
2,∴x
2+(a-3)x-3a>0,
∴(x-3)(x+a)>0对x∈[1,2]恒成立,
又∵x-3<0恒成立,∴x+a<0对x∈[1,2]恒成立,
∴a<-x,又-x∈[-2,-1],
∴a<-2.
(2)由△=(a-3)
2-4(a
2-3a)≥0得:-1≤a≤3,
不妨设a=p,则q,r恰为方程两根,由韦达定理得:
①p+q+r=3,qr=a
2-3a,
②p
2+q
2+r
2=a
2+(q+r)
2-2pr=a
2+(3-a)
2-2(a
2-3a)=9,
③p
3+q
3+r
3=a
3+(q
3+r
3)=a
3+(q+r)[q
2-qr+r
2]=3a
3-9a
2+27.
设g(a)=3a
3-9a
2+27,求导得:g(a)=9a
2-18a=9a(a-2),
当a∈[2,3]时,g(a)>0,g(a)递增;当a∈[0,2]时,g(a)<0,g(a)递减;
当a∈[-1,0]时,g(a)>0,g(a)递增,
∴g(a)在[-1,3]上的最小值为min{g(-1),g(2)}=min{15,15}=15.
(3)由(2)得
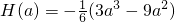
,
如果a∈(0,1),则
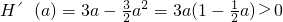
,∴H(a)在(0,1)为递增函数,
易知H(a)∈(0,1),∴a
1∈(0,1)?a
2∈(0,1),a
n∈(0,1)?a
n+1∈(0,1),
又∵

,
∴a
n+1<a
n.
分析:(1)由f(x)>a
2,可得x
2+(a-3)x-3a>0,所以(x-3)(x+a)>0对x∈[1,2]恒成立,又x-3<0恒成立,可得x+a<0对x∈[1,2]恒成立,得出a<-x,又-x∈[-2,-1],即可求出a的取值范围;
(2)由△=(a-3)
2-4(a
2-3a)≥0得:-1≤a≤3,不妨设a=p,则q,r恰为方程两根,由韦达定理讨论即可得出答案.
(3)由(2)得
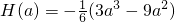
,通过求导数的方法即可求出函数的单调区间,再根据数列的知识即可求解.
点评:本题考查了函数的恒成立问题及数列的应用,难度较大,关键是掌握用导数求函数的单调区间.

 ,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.
,数列{an}满足an+1=H(an)(n∈N*),且a1∈(0,1),试判断an+1与an的大小,并证明之.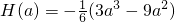 ,
,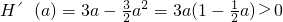 ,∴H(a)在(0,1)为递增函数,
,∴H(a)在(0,1)为递增函数, ,
,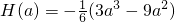 ,通过求导数的方法即可求出函数的单调区间,再根据数列的知识即可求解.
,通过求导数的方法即可求出函数的单调区间,再根据数列的知识即可求解.

 阅读快车系列答案
阅读快车系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<