
已知曲线C: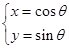 (
(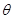 为参数).
为参数).
(1)将C的参数方程化为普通方程;
(2)若把C上各点的坐标经过伸缩变换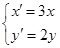 后得到曲线
后得到曲线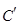 ,求曲线
,求曲线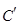 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
科目:高中数学 来源: 题型:解答题
已知在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点
为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点 为极点,
为极点, 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线 的方程为
的方程为 .
.
(Ⅰ)求曲线 直角坐标方程;
直角坐标方程;
(Ⅱ)若曲线 、
、 交于A、B两点,定点
交于A、B两点,定点 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
在平面直角坐标系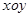 中,直线
中,直线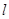 的参数方程为
的参数方程为 (t为参数,α为直线
(t为参数,α为直线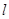 的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.
(1) 若直线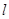 与圆C相切,求
与圆C相切,求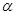 的值;
的值;
(2) 若 直线
直线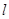 与圆C交与A,B两点,求
与圆C交与A,B两点,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)选修4-4:坐标系与参数方程
已知曲线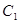 的极坐标方程是
的极坐标方程是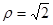 ,曲线
,曲线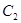 的参数方程是
的参数方程是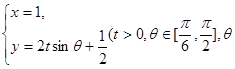 是参数).
是参数).
(1)写出曲线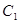 的直角坐标方程和曲线
的直角坐标方程和曲线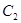 的普通方程;
的普通方程;
(2)求 的取值范围,使得
的取值范围,使得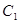 ,
,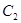 没有公共点.
没有公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出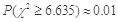 ,则下列说法正确的( )
,则下列说法正确的( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4)(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2)(13,1),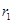 表示变量Y与X之间的线性相关系数,
表示变量Y与X之间的线性相关系数,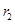 表示变量V与U之间的线性相关系数,则( )
表示变量V与U之间的线性相关系数,则( )
A.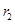 < <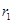 <0 <0 | B.0<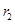 < <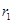 | C.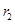 <0< <0<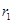 | D.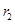 = =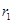 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知某高中高一800名学生某次考试的数学成绩,现在想知道不低于120分,90~
120分,75~90分,60~75分,60分以下的学生分别占多少,需要做的工作是( )
| A.抽取样本,据样本估计总体 | B.求平均成绩 |
| C.进行频率分布 | D.计算方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com