
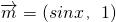 ,
,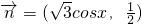 ,函数
,函数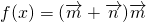 .
.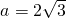 ,c=4且f(A)是函数f(x)在
,c=4且f(A)是函数f(x)在 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S.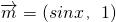 ,
,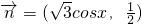 ,
, +
+ =(sinx+
=(sinx+ cosx,
cosx, ),
), +
+ )•
)• =sin2x+
=sin2x+ sinxcosx+
sinxcosx+
 (1-cos2x)+
(1-cos2x)+ sin2x+
sin2x+ =
= sin2x-
sin2x- cos2x+2=sin(2x-
cos2x+2=sin(2x- )+2,
)+2, =π;
=π; ≤2x-
≤2x- ≤2kπ+
≤2kπ+ (k∈Z),解得:kπ-
(k∈Z),解得:kπ- ≤x≤kπ+
≤x≤kπ+ (k∈Z),
(k∈Z), ,kπ+
,kπ+ ](k∈Z);
](k∈Z); )+2,
)+2, ],∴2A-
],∴2A- ∈[-
∈[- ,
, ],
], ≤sin(2A-
≤sin(2A- )≤1,即
)≤1,即 ≤f(A)≤3,
≤f(A)≤3, =
= ,即A=
,即A= 时,f(A)的最大值为3,
时,f(A)的最大值为3, ,c=4,cosA=
,c=4,cosA= ,
, bcsinA=
bcsinA= ×2×4×
×2×4× =2
=2 .
. +
+ 的坐标,然后利用平面向量的数量积运算法则计算,列出函数f(x)的解析式,利用二倍角的正弦、余弦函数公式化简,整理后再利用特殊角的三角函数值及两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式T=
的坐标,然后利用平面向量的数量积运算法则计算,列出函数f(x)的解析式,利用二倍角的正弦、余弦函数公式化简,整理后再利用特殊角的三角函数值及两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式T=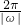 ,即可求出函数的最小正周期;由正弦函数的单调增区间为]2kπ-
,即可求出函数的最小正周期;由正弦函数的单调增区间为]2kπ- ,2kπ+
,2kπ+ ](k∈Z),列出关于x的不等式,求出不等式的解集得到x的范围,即为函数f(x)的单调增区间;
](k∈Z),列出关于x的不等式,求出不等式的解集得到x的范围,即为函数f(x)的单调增区间;

 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源:2011届广东省实验中学、华师附中、深圳中学、广雅中学高三上学期期末数学文卷 题型:解答题
(本小题满分12分)
已知向量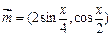 ,
, ,函数
,函数
(1)求 的最小正周期;
的最小正周期;
(2)若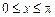 ,求
,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省六校教育研究会高三2月联考理科数学试卷(解析版) 题型:解答题
已知向量 ,
, ,函数
,函数
(Ⅰ)求 的最大值;
的最大值;
(Ⅱ)在 中,设角
中,设角 ,
, 的对边分别为
的对边分别为 ,若
,若 ,且
,且 ?,求角
?,求角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省广州市育才中学高三(上)10月月考数学试卷(文科)(解析版) 题型:解答题
 ,
, ,函数
,函数 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省五校高三下学期第二次联考理科数学试卷(解析版) 题型:解答题
已知向量 ,
, ,函数
,函数 .
.
(Ⅰ)若方程 在
在 上有解,求
上有解,求 的取值范围;
的取值范围;
(Ⅱ)在 中,
中, 分别是A,B,C所对的边,当(Ⅰ)中的
分别是A,B,C所对的边,当(Ⅰ)中的 取最大值且
取最大值且 时,求
时,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2010年南安一中高一下学期期末考试数学卷 题型:解答题
(本小题满分12分)
已知向量 ,
, ,函数
,函数 .
.
(1)求函数 的最小正周期以及单调递增区间;
的最小正周期以及单调递增区间;
(2)若 时, 求
时, 求 的值域;
的值域;
(3)求方程 在
在 内的所有实数根之和.
内的所有实数根之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com