
【题目】如图所示,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() .
.

(I)证明:![]() 平面
平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.
(1)若直线l的倾斜角为60°,求|AB|的值;
(2)若|AB|=9,求线段AB的中点M到准线的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四面体ABCD的体积为1,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体的公共部分的体积为( )
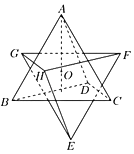
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的一次真假游戏的有奖竞猜中,设置了“科技”和“生活”这两类试题,规定每位职工最多竞猜3次,每次竞猜的结果相互独立.猜中一道“科技”类试题得4分,猜中一道“生活”类试题得2分,两类试题猜不中的都得0分.将职工得分逐次累加并用X表示,如果X的值不低于4分就认为通过游戏的竞猜,立即停止竞猜,否则继续竞猜,直到竞猜完3次为止.竞猜的方案有以下两种:方案1:先猜一道“科技”类试题,然后再连猜两道“生活”类试题;
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距与短轴长相等,椭圆上一点
的焦距与短轴长相等,椭圆上一点![]() 到两焦点距离之差的最大值为4.
到两焦点距离之差的最大值为4.
(1)求椭圆的标准方程;
(2)若点![]() 为椭圆上异于左右顶点
为椭圆上异于左右顶点![]() ,
,![]() 的任意一点,过原点
的任意一点,过原点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一个各个面上均涂有颜色的正方体锯成![]() 个同样大小的小正方体,从这些小正方体中任意取两个,这两个都恰是两面涂色的概率是( )
个同样大小的小正方体,从这些小正方体中任意取两个,这两个都恰是两面涂色的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com