
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是 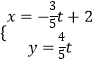 (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,求a的值.
倍,求a的值.
【答案】
(1)解:当a=2时,圆C的直角坐标方程为x2+y2=2y,即x2+(y﹣1)2=1.∴圆C的圆心坐标为C(0,1),半径r=1.
令y= ![]() =0得t=0,把t=0代入x=﹣
=0得t=0,把t=0代入x=﹣ ![]() 得x=2.∴M(2,0).
得x=2.∴M(2,0).
∴|MC|= ![]() =
= ![]() .∴|MN|的最大值为|MC|+r=
.∴|MN|的最大值为|MC|+r= ![]()
(2)解:由ρ=asinθ得ρ2=aρsinθ,∴圆C的直角坐标方程是x2+y2=ay,即x2+(y﹣ ![]() )2=
)2= ![]() .
.
∴圆C的圆心为C(0, ![]() ),半径为|
),半径为| ![]() |,
|,
直线l的普通方程为4x+3y﹣8=0.
∵直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,
倍,
∴圆心C到直线l的距离为圆C半径的一半.
∴ ![]() =|
=| ![]() |,解得a=32或a=
|,解得a=32或a= ![]()
【解析】(1)求出圆C的圆心和半径,M点坐标,则|MN|的最大值为|MC|+r;(2)由垂径定理可知圆心到直线l的距离为半径的 ![]() ,列出方程解出.
,列出方程解出.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2 , 这两条曲线在第一象限的交点为P,△PF1F2 是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2 , 则e1e2 的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行如图所示的程序框图,则“3<m<5”是“输出i的值为5”的( ) 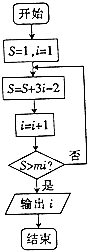
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)=![]() ,则关于x的函数F(x)=f(x)-a(0<a<1,a为常数)的所有零点之和为______.
,则关于x的函数F(x)=f(x)-a(0<a<1,a为常数)的所有零点之和为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为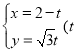 为参数),P、Q分别为直线
为参数),P、Q分别为直线![]() 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,![]() 轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但蔬菜上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水![]() (单位:千克)清洗蔬菜1千克后,蔬菜上残留的农药
(单位:千克)清洗蔬菜1千克后,蔬菜上残留的农药![]() (单位:微克)的统计表:
(单位:微克)的统计表:
| 1 | 2 | 3 | 4 | 5 |
| 58 | 54 | 39 | 29 | 10 |

(1)在答题纸的坐标系中,描出散点图,并判断变量![]() 与
与![]() 是正相关还是负相关;
是正相关还是负相关;
(2)若用解析式![]() 作为蔬菜农药残量
作为蔬菜农药残量![]() 与用水量
与用水量![]() 的回归方程,令
的回归方程,令![]() ,计算平均值
,计算平均值![]() 与
与![]() ,完成以下表格(填在答题卡中),求出
,完成以下表格(填在答题卡中),求出![]() 与
与![]() 的回归方程.(
的回归方程.(![]() ,
, ![]() 保留两位有效数字):
保留两位有效数字):
| 1 | 4 | 9 | 16 | 25 |
| 58 | 54 | 39 | 29 | 10 |
| |||||
|
(3)对于某种残留在蔬菜上的农药,当它的残留量低于20微克时对人体无害,为了放心食用该蔬菜,请评估需要用多少千克的清水清洗一千克蔬菜?(精确到0.1,参考数据![]() )(附:对于一组数据
)(附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:  ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com