A
分析:先求出函数y=e
ax-2x的导数,则当导数等于0时,得到的x的值为函数的极值点,因为函数有大于0的极值点,所以由导数等于0得到的关于x的方程有正根,再用图象法判断出a的范围即可.
解答:∵y=e
ax-2x,∴y′=ae
ax-2,
∵函数有大于零的极值点,
∴y′=0有正根,即ae
ax-2=0有正根
也即函数y=ae
ax与函数y=2的图象交点横坐标大于0
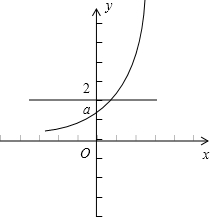
,则交点必在y轴右侧.
若a为负值,则y=ae
ax的图象在x轴下方,与直线y=2无交点,不符合题意.
若a为正值,函数y=ae
ax图象如右图所示,
∵函数y=ae
ax与y轴交于点(0,a),若要与直线y=2交于y轴右侧,则(0,a)点在直线y=2下方,∴a<2,
又∵a>0.
∴0<a<2
故选A
点评:本题主要考查应用导数求函数的极值点,以及图象法判断方程的根的分布.

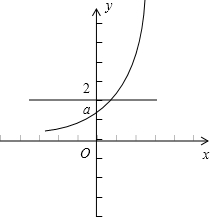 ,则交点必在y轴右侧.
,则交点必在y轴右侧.
