
【题目】记![]() 表示大于
表示大于![]() 的整数
的整数![]() 的十位数,例如
的十位数,例如![]() ,
,![]() .已知
.已知![]() ,
,![]() ,
,![]() 都是大于
都是大于![]() 的互不相等的整数,现有如下
的互不相等的整数,现有如下![]() 个命题:
个命题:
①若![]() ,则
,则![]() ;②
;②![]() ,
,![]() 且
且![]() ;
;
③若![]() 是质数,则
是质数,则![]() 也是质数;④若
也是质数;④若![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() ,
,![]() ,
,![]() 可能成等比数列.
可能成等比数列.
其中所有的真命题为( )
A. ② B. ③④ C. ①②④ D. ①②③④
科目:高中数学 来源: 题型:
【题目】我校高二年级共2000名学生,其中男生1200人.为调查学生们的手机使用情况,采用分层抽样的方法,随机抽取100位学生每周平均使用手机上网时间的样本数据(单位:小时).根据这100个数据,得到学生每周平均使用手机上网时间的频率分布直方图(如图所示),其中样本数据分组区间分别为![]() .
.
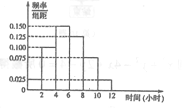
(1)应收集男生、女生样本数据各多少人?
(2)估计我校高二年级学生每周平均使用手机上网时间超过4小时的概率.
(3)将平均每周使用手机上网时间在![]() 内定义为“长时间使用手机”,在
内定义为“长时间使用手机”,在![]() 内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
内定义为“短时间使用手机”.在样本数据中,有25名学生不近视.请完成下列2×2列联表,并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.
近视 | 不近视 | 合计 | |
长时间使用手机上网 | |||
短时间使用手机上网 | 15 | ||
合计 | 25 |
附:![]()
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某共享单车运营公司![]() 为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为
为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为![]() 元/辆和
元/辆和![]() 元/辆的
元/辆的![]() 、
、![]() 两款车型可供选择,按规定每辆单车最多使用
两款车型可供选择,按规定每辆单车最多使用![]() 年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各
年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各![]() 辆进行科学模拟测试,得到两款单车使用寿命频数表见下表.
辆进行科学模拟测试,得到两款单车使用寿命频数表见下表.

经测算,平均每辆单车每年可以带来收入![]() 元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整年.
元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整年.
(1)分别估计![]() 、
、![]() 两款车型使用寿命不低于
两款车型使用寿命不低于![]() 年的概率;
年的概率;
(2)如果你是![]() 公司的负责人,以参加科学模拟测试的两款车型各
公司的负责人,以参加科学模拟测试的两款车型各![]() 辆单车产生利润的平均数为决策依据,你会选择采购哪款车型?
辆单车产生利润的平均数为决策依据,你会选择采购哪款车型?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]() (
(![]() ,
,![]() )图象上的任意两点,且角
)图象上的任意两点,且角![]() 的终边经过点
的终边经过点![]() ,若
,若![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中,曲线
中,曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016~2017·郑州高一检测)过点M(1,2)的直线l与圆C:(x-3)2+(y-4)2=25交于A,B两点,C为圆心,当∠ACB最小时,直线l的方程是 ( )
A. x-2y+3=0 B. 2x+y-4=0
C. x-y+1=0 D. x+y-3=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ![]() )的周期为π,且图象上的一个最低点为M(
)的周期为π,且图象上的一个最低点为M(![]() ).
).
(1)求f(x)的解析式及单调递增区间;
(2)当x∈[0,![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com