
分析 由已知可得sin(A-$\frac{π}{3}})$)=$\frac{1}{2}$,结合A的范围可求A=$\frac{2π}{3}$,将sin(B-C)=4cosBsinC展开后,转化可得sin(B+C)=6cosBsinC,利用正弦定理、余弦定理得b2=5c2+2bc,从而可得答案.
解答 解:∵2sin(A-$\frac{π}{3}})$)=$\sqrt{3}$,可得:sin(A-$\frac{π}{3}})$)=$\frac{1}{2}$,
∵A∈(0,π),A-$\frac{π}{3}})$∈(-$\frac{π}{3}})$,$\frac{2π}{3}$),
∴A-$\frac{π}{3}})$=$\frac{π}{3}})$,解得:A=$\frac{2π}{3}$.…4分
又∵sin(B-C)=4cosBsinC,
∴sinBcosC-cosBsinC=4cosBsinC,
∴sinBcosC+cosBsinC=6cosBsinC,即sin(B+C)=6cosBsinC,
∵A+B+C=π,
∴sinA=6cosBsinC,由正弦定理、余弦定理得a=6×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$×c,
可得:$\frac{1}{2}$(3b2-3c2)=a2=b2+c2-2bccos$\frac{2π}{3}$=b2+c2+bc,…10分
解得:b2=5c2+2bc,即:($\frac{b}{c}$)2-2•$\frac{b}{c}$-5=0,
∴解得:$\frac{b}{c}$=1+$\sqrt{6}$,或1-$\sqrt{6}$(舍去).
故答案为:$1+\sqrt{6}$.…12分
点评 本题主要考查了正弦定理与余弦定理的综合应用,考查了三角函数恒等变换的应用,考查转化思想与运算求解能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
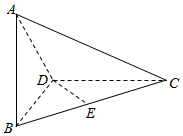 如图,已知三棱锥A-BCD中,DB=DC=BA=2,BD⊥DC,AB⊥平面BCD,E为BC的中点.
如图,已知三棱锥A-BCD中,DB=DC=BA=2,BD⊥DC,AB⊥平面BCD,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )
如图,在菱形ABCD中,∠BAD=60°,AB=2$\sqrt{3}$,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P-BCD的外接球的表面积为( )| A. | 28π | B. | 32π | C. | 16π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有1个黑球和都是红球 | B. | 至少有1个黑球和都是黑球 | ||
| C. | 至少有1个黑球与至少1个红球 | D. | 恰有1个黑球与恰有2个黑球 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={log_{\frac{1}{2}}}x$ | B. | $y=\frac{1}{x}$ | C. | y=-tanx | D. | y=-x3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com