【题目】在△ABC中，sinB+ 
sin 
=1﹣cosB．
（1）求角B的大小；
（2）求sinA+cosC的取值范围．
【答案】
（1）解：由sinB+ 
sin 
=1﹣cosB．
可得：2sin cos + sin =1﹣（1﹣2 
）
2cos + =2sin
=2 sin（ 
）
sin（ ）= 
，
∵0＜B＜π，
∴0＜ ＜π，
∴ 
＜ ＜ 
，
∴sin（ ）=sin 
∴B= 
；
（2）解：由（1）可得B= ，
∴A+C= ，
那么：sinA+cosC=sinA+cos（ ﹣A）= 
sinA 
cosA= 
sin（A+ ），
∵0＜A＜ ，
∴ ＜A+ ＜ 
，
sin（A+ ）∈（ ， 
），
∴sinA+cosC的取值范围是（ ， ）．
【解析】1、由正余弦的二倍角公式可得原式化为sin（ ）= ,根据角的取值范围可得 sin（ ）=sin 既得结果。
2、根据（1）的结论由三角形的内角和可得A+C= ，把要求的式子整理化简得sinA+cosC= 3 sin（A+ ），再根据角的取值范围可得 ＜A+ ＜ ，故得sinA+cosC的取值范围。
【考点精析】认真审题，首先需要了解正弦定理的定义(正弦定理:
)．
科目：高中数学 来源： 题型：
【题目】200名职工年龄分布如图所示，从中随机抽取40名职工作样本，采用系统抽样方式，按1～200编号分为40组，分别为1～5，6～10，…，196～200，第5组抽取号码为23，第9组抽取号码为；若采用分层抽样，40﹣50岁年龄段应抽取人．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的首项a1=1，且an+1=2an+1（n∈N*）
（Ⅰ）证明数列{an+1}是等比数列，并求数列{an}的通项公式；
（Ⅱ）设bn= 
，求数列{bn}的前n项和Sn；
（Ⅲ）在条件（Ⅱ）下对任意正整数n，不等式Sn+ 
﹣1＞（﹣1）na恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ 
）的部分图象如图所示，则（ ）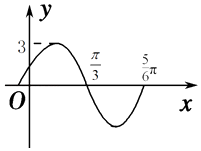
A.f（x）的一个对称中心为 
B.f（x）的图象关于直线 
对称
C.f（x）在 
上是增函数
D.f（x）的周期为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线 
﹣ 
=1（a＞0，b＞0）的左、右焦点分别为F1、F2 ， 过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点，AF2、BF2分别交y轴于P、Q两点，若△PQF2的周长为12，则ab取得最大值时该双曲线的离心率为（ ）
A.
B.
C.2
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
