
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源: 题型:
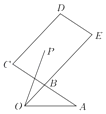
【题目】如图,B是AC的中点,![]() ,P是平行四边形BCDE内(含边界)的一点,且
,P是平行四边形BCDE内(含边界)的一点,且![]() .有以下结论:
.有以下结论:
①当x=0时,y∈[2,3];
②当P是线段CE的中点时,![]() ;
;
③若x+y为定值1,则在平面直角坐标系中,点P的轨迹是一条线段;
④x﹣y的最大值为﹣1;
其中你认为正确的所有结论的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为整数的无穷数列![]() 满足:
满足:![]() ,且对所有
,且对所有![]() ,
,![]() 均成立.
均成立.
(1)写出![]() 的所有可能值(不需要写计算过程);
的所有可能值(不需要写计算过程);
(2)若![]() 是公差为1的等差数列,求
是公差为1的等差数列,求![]() 的通项公式;
的通项公式;
(3)证明:存在满足条件的数列![]() ,使得在该数列中,有无穷多项为2019.
,使得在该数列中,有无穷多项为2019.
查看答案和解析>>
科目:高中数学 来源: 题型:
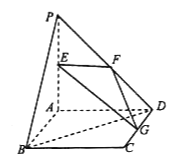
【题目】如图,直线![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,且
是正方形,且![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成角的大小(结果用反三角表示);
所成角的大小(结果用反三角表示);
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一列函数![]() ,设直线
,设直线![]() 与
与![]() 的交点为
的交点为![]() ,点
,点![]() 在
在![]() 轴和直线
轴和直线![]() 上的射影分别为
上的射影分别为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的最小值,并指出此时
的最小值,并指出此时![]() 的取值;
的取值;
(2)在![]() 中任取一个函数,求该函数在
中任取一个函数,求该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的概率;
上是减函数的概率;
(3)是否存在正整数![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若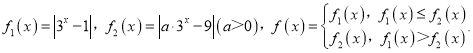
(1)当![]() 时,设
时,设![]() 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为![]() (闭区间
(闭区间![]() 的长度为
的长度为![]() ),试求
),试求![]() 的最大值;
的最大值;
(2)是否存在这样的![]() 使得当
使得当![]() 时,
时,![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为菱形,且∠ABC=60°,
中,底面ABCD为菱形,且∠ABC=60°,![]() 平面ABCD,
平面ABCD,![]() ,点E,F为PC,PA的中点.
,点E,F为PC,PA的中点.
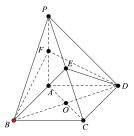
(1)求证:平面BDE⊥平面ABCD;
(2)二面角E—BD—F的大小;
(3)设点M在PB(端点除外)上,试判断CM与平面BDF是否平行,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,如表是该地一建设银行连续五年的储蓄存款(年底余额),如表1
![]()
为了研究计算方便,工作人员将上表的数据进行了处理,令![]() ,
,![]() 得到表2:
得到表2:
![]()
(1)求:![]() 关于t的线性回归方程;
关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测到2019年年底,该地储蓄存款额可达多少?
附:对于线性回归方程![]() ,其中
,其中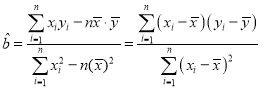 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com