
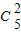 种,故
种,故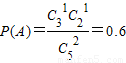 ,可得所求为
,可得所求为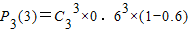 ,运算求得结果.
,运算求得结果.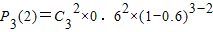 ,运算求得结果.
,运算求得结果.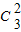 •P(A)•P(A)•P(C),计算可得结果.
•P(A)•P(A)•P(C),计算可得结果.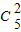 种,故
种,故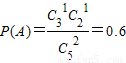 ,
, .…(4分)
.…(4分)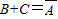 ,∴可以使用n次独立重复试验.
,∴可以使用n次独立重复试验.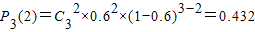 .…(8分)
.…(8分)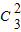 •P(A)•P(A)•P(C)=0.324. …(14分)
•P(A)•P(A)•P(C)=0.324. …(14分)

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆一中(本部)高二(下)期末数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com