
| A. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向左平行移动$\frac{π}{8}$个单位长度 | |
| B. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向左平行移动$\frac{π}{4}$个单位长度 | |
| C. | 横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动$\frac{π}{8}$个单位长度 | |
| D. | 横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动$\frac{π}{4}$个单位长度 |
分析 利用诱导公式化简y=$\sqrt{2}$sin(4x+$\frac{π}{4}$),再根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由于y=$\sqrt{2}$sin(4x+$\frac{π}{4}$)=$\sqrt{2}$cos[$\frac{π}{2}$-(4x+$\frac{π}{4}$)]=$\sqrt{2}$cos(4x-$\frac{π}{4}$),
所以,将函数y=$\sqrt{2}$sin(4x+$\frac{π}{4}$)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),可得:y=$\sqrt{2}$cos(2x-$\frac{π}{4}$)=$\sqrt{2}$cos2(x-$\frac{π}{8}$),
再向左平行移动$\frac{π}{8}$个单位长度,可得y=$\sqrt{2}$cos2[(x+$\frac{π}{8}$)-$\frac{π}{8}$]=$\sqrt{2}$cos2x的图象.
故选:C.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
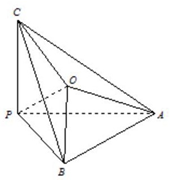 如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )
如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPC=45°,∠OPA=60°,则∠OPB的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=2 | B. | (x-1)2+y2=4 | C. | y2=2x | D. | y2=-2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com