
【题目】已知抛物线![]() 的焦点为F,过F作平行于x轴的直线交抛物线于A,B两点(A在B的左侧),若△AOB的面积为2.
的焦点为F,过F作平行于x轴的直线交抛物线于A,B两点(A在B的左侧),若△AOB的面积为2.
(1)求抛物线C的方程;
(2)设P是抛物线C的准线上一点,Q是抛物线上的一点,若PF⊥QF,求证:直线PQ与抛物线相切.

【答案】(1) ![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)由题意可得![]() ,则
,则![]() |由
|由![]() ,可得
,可得![]() ,从而可得结果;(2)设
,从而可得结果;(2)设![]() ,显然
,显然![]() 时不满足题意. 当
时不满足题意. 当![]() 时,
时,![]() .又直线
.又直线![]() 的方程为
的方程为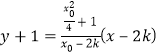 ,将
,将![]() 代入整理得
代入整理得![]() ,则
,则![]() 或
或![]() ,而
,而![]() ,则
,则![]() ,所以
,所以![]() ,从而可得结论.
,从而可得结论.
(1)由题意可得![]() ,则|AB|=2p,△AOB的面积
,则|AB|=2p,△AOB的面积![]() ,所以p=2,则抛物线C的方程为
,所以p=2,则抛物线C的方程为![]() .
.
(2)证明:显然FQ的斜率存在,设为k,当k=0时,P(0,-1,Q(2,1)或(-2,1),直线![]() 或y=-x-1,与抛物线
或y=-x-1,与抛物线![]() 联立,得判别式△=0,所以此时直线与抛物线C相切;当k≠0时,设直线
联立,得判别式△=0,所以此时直线与抛物线C相切;当k≠0时,设直线![]() ,
,
因为PF⊥QF,则直线PF的方程为![]() ,
,
由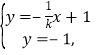 得P(2k,- 1),
得P(2k,- 1),![]() 消去y得
消去y得![]() ,
,
由Q是直线FQ与抛物线C的交点,
设![]() ,显然
,显然![]() 时不满足题意.
时不满足题意.
当![]() 时,
时,![]() .
.
又直线PQ的方程为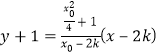 ,将
,将![]() ,即
,即![]() 代入整理得
代入整理得![]() ,
,
则![]() 或
或![]() ,而
,而![]() ,则
,则![]() ,
,
所以![]() ,故直线PQ与抛物线C相切.·
,故直线PQ与抛物线C相切.·


科目:高中数学 来源: 题型:
【题目】某校高一年级3个班有10名学生在全国英语能力大赛中获奖,学生来源人数如表:
班别 | 高一(1)班 | 高一(2)班 | 高一(3)班 |
人数 | 3 | 6 | 1 |
若要求从10位同学中选出两位同学介绍学习经验,设其中来自高一(1)班的人数为ξ,求随机变量ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品.统计结果如下:
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水线样本的频率分布直方图
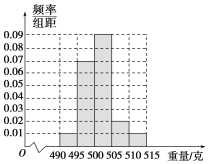
(1)求甲流水线样本合格的频率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年存节期间,某服装超市举办了一次有奖促销活动,消费每超过600 元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种. 方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸到2个红球,则打6折;若摸到1个红球,则打7折;若没摸到红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了 600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左焦点为F,直线y=kx(k>0)与椭圆C交于A,B两点,若
=1(a>b>0)的左焦点为F,直线y=kx(k>0)与椭圆C交于A,B两点,若 ![]() ,则C的离心率取值范围为( )
,则C的离心率取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体ABCDE中,△BCD是边长为2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中点. 
(Ⅰ)求证:BF⊥CD;
(Ⅱ)求二面角C﹣BF﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,定义域为[0,2π],g(x) 为f(x) 的导函数.
,定义域为[0,2π],g(x) 为f(x) 的导函数.
(1)求方程g(x)=0 的解集;
(2)求函数g(x) 的最大值与最小值;
(3)若函数F(x)=f(x)﹣ax 在定义域上恰有2个极值点,求实数a 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:m∈R,且m+1≤0,q:x∈R,x2+mx+1>0恒成立,若p∧q为假命题且p∨q为真命题,则m的取值范围是__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com