
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且方程
,且方程![]() 在
在![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(2)
.(2)![]()
【解析】【试题分析】(1)先求出函数解析式导数,再借助导数与函数的单调性的关系求解;(2)依据题设先将问题进行等价转化,再构造函数运用导数与函数的单调性的关系研究函数的图像的形状分析求解:
(1)若![]() ,
, ![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
,
①若![]() ,即
,即![]() 时,
时, ![]() ,此时函数单调递减,单调递减区间为
,此时函数单调递减,单调递减区间为![]() ;
;
②若![]() ,即
,即![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() 得
得![]() ,或
,或![]() ,
,
所以单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)若![]() ,∴
,∴![]() ,
, ![]() 则,
则,
若方程![]() 在
在![]() 内有解,即
内有解,即![]() 在
在![]() 内有解,
内有解,
即![]() 在
在![]() 有解.
有解.
设![]() ,则
,则![]() 在
在![]() 内有零点,设
内有零点,设![]() 是
是![]() 在
在![]() 内的一个零点,
内的一个零点,
因为![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上不可能单调,
上不可能单调,
由![]() ,设
,设![]() ,则
,则![]() 在
在![]() 和
和![]() 上存在零点,
上存在零点,
即![]() 在
在![]() 上至少有两个零点,因为
上至少有两个零点,因为![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递增,不合题意;
上递增,不合题意;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递减,不合题意;
上递减,不合题意;
当![]() 时,令
时,令![]() ,得
,得![]() ,则
,则![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
![]() 在
在![]() 上存在最小值
上存在最小值![]() .
.
若![]() 有两个零点,则有
有两个零点,则有![]() ,
, ![]() .
.
所以![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递增;
递增;
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递减,
递减,
则![]() ,所以
,所以![]() 恒成立.
恒成立.
由![]() ,
, ![]() ,所以
,所以![]() ,
,
当![]() 时,设
时,设![]() 的两个零点为
的两个零点为![]() ,
,
则![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
则![]() ,
, ![]() ,则
,则![]() 在
在![]() 内有零点,
内有零点,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若曲线![]() 在
在![]() 轴上的截距为-1,且在点
轴上的截距为-1,且在点![]() 处的切线垂直于直线
处的切线垂直于直线![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)记![]() 的导函数为
的导函数为![]() ,
, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)由数字1、2、3、4、5、6、7组成无重复数字的七位数
求三个偶数必相邻的七位数的个数及三个偶数互不相邻的七位数的个数
(2)六本不同的书,分为三组,求在下列条件下各有多少种不同的分配方法?
(I)每组两本
(II)一组一本,一组二本,一组三本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题。”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论。现从该班随机抽取5位学生在一次考试中的数学和物理成绩,如下表:

(1)求数学成绩y对物理成绩x的线性回归方程![]() 。若某位学生的物理成绩为80分,预测他的数学成绩;
。若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这5位学生中随机抽取2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率。(参考公式: 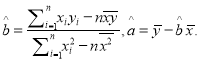 参考数据:
参考数据: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() ),圆
),圆![]() (
(![]() ),若圆
),若圆![]() 的一条切线
的一条切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)当![]() ,
, ![]() 时,若点
时,若点![]() 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,探究
,探究![]() 之间的等量关系,并说明理由.
之间的等量关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() 在曲线
在曲线![]() 上,若直线
上,若直线![]() 的斜率
的斜率![]() 满足
满足![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com