
ΓΨΧβΡΩΓΩΡ≥ΗΏΥΌΙΪ¬Ζ»Ϊ≥Χ…η”–2n(nΓί4Θ§![]() )ΗωΖΰΈώ«χ.ΈΣΦ”«ΩΦί Μ»Υ‘±ΒΡΑ≤»Ϊ“β ΕΘ§œ÷ΙφΜ°‘ΎΟΩΗωΖΰΈώ«χΒΡ»κΩΎ¥Π…η÷Ο–―ΡΩΒΡ–ϊ¥Ϊ±ξ”οAΜρ–ϊ¥Ϊ±ξ”οB.
)ΗωΖΰΈώ«χ.ΈΣΦ”«ΩΦί Μ»Υ‘±ΒΡΑ≤»Ϊ“β ΕΘ§œ÷ΙφΜ°‘ΎΟΩΗωΖΰΈώ«χΒΡ»κΩΎ¥Π…η÷Ο–―ΡΩΒΡ–ϊ¥Ϊ±ξ”οAΜρ–ϊ¥Ϊ±ξ”οB.
Θ®1Θ©»τΟΩΗωΖΰΈώ«χ»κΩΎ¥Π…η÷Ο–ϊ¥Ϊ±ξ”οAΒΡΗ≈¬ ΈΣ![]() Θ§»κΩΎ¥Π…η÷Ο–ϊ¥Ϊ±ξ”οBΒΡΖΰΈώ«χ”–XΗωΘ§«σXΒΡ ΐ―ßΤΎΆϊΘΜ
Θ§»κΩΎ¥Π…η÷Ο–ϊ¥Ϊ±ξ”οBΒΡΖΰΈώ«χ”–XΗωΘ§«σXΒΡ ΐ―ßΤΎΆϊΘΜ
Θ®2Θ© ‘ΧΫΨΩ»Ϊ≥ΧΝΫ÷÷–ϊ¥Ϊ±ξ”οΒΡ…η÷Ο±»άΐΘ§ ΙΒΟ≥ΛΆΨΥΨΜζ‘ΎΉΏΗΟΗΏΥΌ»Ϊ≥Χ÷–Θ§ΥφΜζ―Γ»Γ3ΗωΖΰΈώ«χ–ίœΔΘ§Ω¥ΒΫœύΆ§–ϊ¥Ϊ±ξ”οΒΡΗ≈¬ Ήν–ΓΘ§≤Δ«σ≥ωΤδΉν–Γ÷Β.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®2Θ©ΝΫ÷÷–ϊ¥Ϊ±ξ”ο1ΘΚ1…η÷Ο ±Θ§ΖϊΚœΧβ…ηΒΡΗ≈¬ Ήν–ΓΘ§ΤδΉν–Γ÷ΒΈΣ
Θ®2Θ©ΝΫ÷÷–ϊ¥Ϊ±ξ”ο1ΘΚ1…η÷Ο ±Θ§ΖϊΚœΧβ…ηΒΡΗ≈¬ Ήν–ΓΘ§ΤδΉν–Γ÷ΒΈΣ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Χβ“βΒΟΟΩΗωΖΰΈώ«χ»κΩΎ¥Π…η÷Ο–ϊ¥Ϊ±ξ”οBΒΡΗ≈¬ ΈΣ![]() Θ§‘ρX~B(2nΘ§
Θ§‘ρX~B(2nΘ§![]() )Θ§”…¥ΥΩ…«σ≥ω¥πΑΗΘΜ
)Θ§”…¥ΥΩ…«σ≥ω¥πΑΗΘΜ
Θ®2Θ©”…Ι≈ΒδΗ≈–ΆΒΡΗ≈¬ ΦΤΥψΙΪ ΫΩ…ΒΟΘ§Φ«’β3ΗωΖΰΈώ«χΩ¥ΒΫœύΆ§ΒΡ–ϊ¥Ϊ±ξ”οΒΡ ¬Φΰ ΐΈΣMΘ§Ω¥ΒΫœύΆ§–ϊ¥Ϊ±ξ”οΒΡΗ≈¬ PΘΫ![]() Θ§ …ηΗΟΗΏΥΌΙΪ¬Ζ»Ϊ≥Χ2nΗωΖΰΈώ«χ÷–Θ§»κΩΎ¥Π…η÷Ο–―ΡΩΒΡ–ϊ¥Ϊ±ξ”οAΒΡ”–m(m
Θ§ …ηΗΟΗΏΥΌΙΪ¬Ζ»Ϊ≥Χ2nΗωΖΰΈώ«χ÷–Θ§»κΩΎ¥Π…η÷Ο–―ΡΩΒΡ–ϊ¥Ϊ±ξ”οAΒΡ”–m(m![]() Θ§mΓή2n)ΗωΘ§Ζ÷άύΧ÷¬έΘ§άϊ”Ο ΐΝ–÷–ΝΎœνΉς≤νΖ®Θ®Φ¥ΗυΨίœύΝΎΝΫœν÷°≤νΒΡΖϊΚ≈≈–ΕœΤδΒΞΒς–‘Θ©ΫαΚœΉιΚœ ΐΒΡ–‘÷ Ω…«σΒΟ
Θ§mΓή2n)ΗωΘ§Ζ÷άύΧ÷¬έΘ§άϊ”Ο ΐΝ–÷–ΝΎœνΉς≤νΖ®Θ®Φ¥ΗυΨίœύΝΎΝΫœν÷°≤νΒΡΖϊΚ≈≈–ΕœΤδΒΞΒς–‘Θ©ΫαΚœΉιΚœ ΐΒΡ–‘÷ Ω…«σΒΟ![]() ΒΡΉν–Γ÷ΒΘ§¥”Εχ«σ≥ω¥πΑΗΘ°
ΒΡΉν–Γ÷ΒΘ§¥”Εχ«σ≥ω¥πΑΗΘ°
ΫβΘΚΘ®1Θ©ΓΏΟΩΗωΖΰΈώ«χ»κΩΎ¥Π…η÷Ο–ϊ¥Ϊ±ξ”οAΒΡΗ≈¬ ΈΣ![]() Θ§
Θ§
ΓύΟΩΗωΖΰΈώ«χ»κΩΎ¥Π…η÷Ο–ϊ¥Ϊ±ξ”οBΒΡΗ≈¬ ΈΣ![]() Θ§
Θ§
ΓύX~B(2nΘ§![]() )Θ§Γύ
)Θ§Γύ![]() ΘΜ
ΘΜ
Θ®2Θ©≥ΛΆΨΥΨΜζ‘ΎΉΏΗΟΗΏΥΌ»Ϊ≥Χ÷–Θ§ΥφΜζΒΡ―Γ»Γ3ΗωΖΰΈώ«χΘ§Ι≤”–![]() ÷÷―Γ»ΓΖΫΖ®Θ§
÷÷―Γ»ΓΖΫΖ®Θ§
≥ΛΆΨΥΨΜζ‘ΎΉΏΗΟΗΏΥΌ»Ϊ≥Χ÷–Θ§ΥφΜζΒΡ―Γ»Γ3ΗωΖΰΈώ«χΘ§
Φ«’β3ΗωΖΰΈώ«χΩ¥ΒΫœύΆ§ΒΡ–ϊ¥Ϊ±ξ”οΒΡ ¬Φΰ ΐΈΣMΘ§
‘ρΤδΗ≈¬ PΘΫ![]() Θ§
Θ§
…ηΗΟΗΏΥΌΙΪ¬Ζ»Ϊ≥Χ2nΗωΖΰΈώ«χ÷–Θ§»κΩΎ¥Π…η÷Ο–―ΡΩΒΡ–ϊ¥Ϊ±ξ”οAΒΡ”–m(m![]() Θ§mΓή2n)ΗωΘ§
Θ§mΓή2n)ΗωΘ§
ΔΌΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Νν![]() Θ§
Θ§![]() Θ§
Θ§
‘ρΒ±![]() ±Θ§
±Θ§![]()
![]()
![]() Θ§
Θ§
ΓύΒ±![]() ±Θ§
±Θ§![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
ΓύΒ±![]() ±Θ§
±Θ§![]() Θ§Φ¥
Θ§Φ¥![]() ΘΜ
ΘΜ
ΔΎΒ±![]() Θ§
Θ§![]() ±Θ§
±Θ§![]() Θ§œ‘»Μ
Θ§œ‘»Μ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏ![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
Γύ![]()
![]()
![]() Θ§
Θ§
Φ¥![]() Θ§
Θ§
Β±![]() Θ§
Θ§![]() ±Θ§
±Θ§![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§![]() ±Θ§
±Θ§![]() Θ§Μρ
Θ§Μρ![]() Θ§Μρ
Θ§Μρ![]() Θ§
Θ§
ΓύΆ§ΔΎΘ§![]() ΘΜ
ΘΜ
Ήέ…œΘ§Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§![]() Θ§
Θ§
Φ¥ΝΫ÷÷–ϊ¥Ϊ±ξ”ο1ΘΚ1…η÷Ο ±Θ§ΖϊΚœΧβ…ηΒΡΗ≈¬ Ήν–ΓΘ§ΤδΉν–Γ÷ΒΈΣ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“ΙζΙ≈¥ζ ΐ―ßΟϊ÷χΓΕΥψΖ®Ά≥ΉΎΓΖ÷–”–»γœ¬Έ ΧβΘΚΓΑ‘ΕΆϊΈΓΈΓΥΰΤΏ≤ψΘ§ΚλΙβΒψΒψ±ΕΦ”‘ωΘ§Ι≤ΒΤ»ΐΑΌΑΥ °“ΜΘ§«κΈ ΦβΆΖΦΗ’ΒΒΤΘΩΓ±“βΥΦ «ΘΚ“ΜΉυ7≤ψΥΰΙ≤Ι“ΝΥ381’ΒΒΤΘ§«“œύΝΎΝΫ≤ψ÷–ΒΡœ¬“Μ≤ψΒΤ ΐ «…œ“Μ≤ψΒΤ ΐΒΡ2±ΕΘ§‘ρΥΰΒΡΕΞ≤ψΙ≤”–ΒΤΘ® Θ©
A. 1’Β B. 3’Β C. 5’Β D. 9’Β
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡΫΙΨύΈΣ4Θ°«“ΙΐΒψ
ΒΡΫΙΨύΈΣ4Θ°«“ΙΐΒψ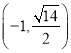 Θ°
Θ°
Θ®1Θ©«σΆ÷‘≤EΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΙΐBΒψ«“–±¬ ΈΣ
Θ§ΙΐBΒψ«“–±¬ ΈΣ![]() ΒΡ÷±œΏlΫΜΆ÷‘≤E”ΎΝμ“ΜΒψMΘ§ΫΜx÷α”ΎΒψQΘ§÷±œΏAM”κ÷±œΏ
ΒΡ÷±œΏlΫΜΆ÷‘≤E”ΎΝμ“ΜΒψMΘ§ΫΜx÷α”ΎΒψQΘ§÷±œΏAM”κ÷±œΏ![]() œύΫΜ”ΎΒψPΘ°÷ΛΟςΘΚ
œύΫΜ”ΎΒψPΘ°÷ΛΟςΘΚ![]() Θ®OΈΣΉχ±ξ‘≠ΒψΘ©Θ°
Θ®OΈΣΉχ±ξ‘≠ΒψΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΦΪΉχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() Θ§…η
Θ§…η![]() ”κ
”κ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§
ΝΫΒψΘ§![]() ÷–ΒψΈΣ
÷–ΒψΈΣ![]() Θ§
Θ§![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ
ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ![]() ”Ύ
”Ύ![]() ΓΔ
ΓΔ![]() .“‘
.“‘![]() ΈΣΉχ±ξ‘≠ΒψΘ§ΦΪ÷αΈΣ
ΈΣΉχ±ξ‘≠ΒψΘ§ΦΪ÷αΈΣ![]() ÷αΒΡ’ΐΑκ÷αΫ®ΝΔ÷±Ϋ«Ήχ±ξœΒ
÷αΒΡ’ΐΑκ÷αΫ®ΝΔ÷±Ϋ«Ήχ±ξœΒ![]() .
.
Θ®1Θ©«σ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥Χ”κΒψ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥Χ”κΒψ![]() ΒΡ÷±Ϋ«Ήχ±ξΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΘΜ
Θ®2Θ©«σ÷ΛΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ρ≥ΒΊ”–“ΜΩιΑκΨΕΈΣRΒΡ…»–ΈAOBΙΪ‘ΑΘ§Τδ÷–OΈΣ…»–ΈΥυ‘Ύ‘≤ΒΡ‘≤–ΡΘ§AOBΘΫ![]() Θ§OAΘ§OBΘ§
Θ§OAΘ§OBΘ§![]() ΈΣΙΪ‘Α‘≠”–Βά¬Ζ.ΈΣ¬ζΉψ –ΟώΙέ…ΆΚΆΫΓ…μΒΡ–η“ΣΘ§ –’ΰ≤ΩΟ≈Ρβ‘Ύ
ΈΣΙΪ‘Α‘≠”–Βά¬Ζ.ΈΣ¬ζΉψ –ΟώΙέ…ΆΚΆΫΓ…μΒΡ–η“ΣΘ§ –’ΰ≤ΩΟ≈Ρβ‘Ύ![]() …œ―ûÓΜΒψMΘ§–¬Ϋ®Βά¬ΖOMΦΑ”κOAΤΫ––ΒΡΒά¬ΖMNΘ®ΒψN‘ΎœΏΕΈOB…œΘ©Θ§…ηAOMΘΫ
…œ―ûÓΜΒψMΘ§–¬Ϋ®Βά¬ΖOMΦΑ”κOAΤΫ––ΒΡΒά¬ΖMNΘ®ΒψN‘ΎœΏΕΈOB…œΘ©Θ§…ηAOMΘΫ![]() .
.

Θ®1Θ©»γΚΈ…ηΦΤΘ§≤≈Ρή Ι –Οώ¥”ΒψO≥ωΖΔ―ΊΒά¬ΖOMΘ§MN––ΉΏ÷ΝΒψNΥυΨ≠ΙΐΒΡ¬ΖΨΕΉν≥ΛΘΩ«κΥΒΟςάμ”…ΘΜ
Θ®2Θ©»γΚΈ…ηΦΤΘ§≤≈Ρή Ι –Οώ¥”ΒψA≥ωΖΔ―ΊΒά¬Ζ![]() Θ§MN––ΉΏ÷ΝΒψNΥυΨ≠ΙΐΒΡ¬ΖΨΕΉν≥ΛΘΩ«κΥΒΟςάμ”….
Θ§MN––ΉΏ÷ΝΒψNΥυΨ≠ΙΐΒΡ¬ΖΨΕΉν≥ΛΘΩ«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΨ≠œζΡ≥…ΧΤΖΘ§ΗυΨί“‘ΆυΉ ΝœΆ≥ΦΤΘ§ΙΥΩΆ≤…”ΟΒΡΗΕΩνΤΎ ΐ![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
| 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
…Χ≥ΓΨ≠œζ“ΜΦΰΗΟ…ΧΤΖΘ§≤…”Ο1ΤΎΗΕΩνΘ§Τδάϊ»σΈΣ200‘ΣΘΜΖ÷2ΤΎΜρ3ΤΎΗΕΩνΘ§Τδάϊ»σΈΣ250‘ΣΘΜΖ÷4ΤΎΜρ5ΤΎΗΕΩνΘ§Τδάϊ»σΈΣ300‘ΣΘ§X±μ ΨΨ≠œζ“ΜΦΰΗΟ…ΧΤΖΒΡάϊ»σ.
Θ®1Θ©«σ ¬ΦΰAΘΚΓΑΙΚ¬ρΗΟ…ΧΤΖΒΡ3ΈΜΙΥΩΆ÷–Θ§÷Ν…Ό”–1ΈΜ≤…”Ο1ΤΎΗΕΩνΓ±ΒΡΗ≈¬ ![]() ΘΜ
ΘΜ
Θ®2Θ©«σXΒΡΖ÷≤ΦΝ–ΦΑΤΎΆϊ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() «
«![]() …œΒΡΤφΚ· ΐΘ§Τδ÷–
…œΒΡΤφΚ· ΐΘ§Τδ÷–![]() Θ§‘ρœ¬ Ν–ΙΊ”ΎΚ· ΐ
Θ§‘ρœ¬ Ν–ΙΊ”ΎΚ· ΐ![]() ΒΡΟη ω÷–Θ§Τδ÷–’ΐ»ΖΒΡ «Θ® Θ©
ΒΡΟη ω÷–Θ§Τδ÷–’ΐ»ΖΒΡ «Θ® Θ©
ΔΌΫΪΚ· ΐ![]() ΒΡΆΦœσœρ”“ΤΫ“Τ
ΒΡΆΦœσœρ”“ΤΫ“Τ![]() ΗωΒΞΈΜΩ…“‘ΒΟΒΫΚ· ΐ
ΗωΒΞΈΜΩ…“‘ΒΟΒΫΚ· ΐ![]() ΒΡΆΦœσΘΜ
ΒΡΆΦœσΘΜ
ΔΎΚ· ΐ![]() ΆΦœσΒΡ“ΜΧθΕ‘≥Τ÷αΖΫ≥ΧΈΣ
ΆΦœσΒΡ“ΜΧθΕ‘≥Τ÷αΖΫ≥ΧΈΣ![]() ΘΜ
ΘΜ
ΔέΒ±![]() ±Θ§Κ· ΐ
±Θ§Κ· ΐ![]() ΒΡΉν–Γ÷ΒΈΣ
ΒΡΉν–Γ÷ΒΈΣ![]() ΘΜ
ΘΜ
ΔήΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΞΒςΒί‘ω.
…œΒΞΒςΒί‘ω.
A.ΔΌΔέB.ΔέΔήC.ΔΎΔέD.ΔΎΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐf(x)=aex©¹xΘ§
Θ®1Θ©«σf(x)ΒΡΒΞΒς«χΦδΘ§
Θ®2Θ©»τΙΊ”Ύx≤ΜΒ» ΫaexΓίx+bΕ‘»Έ“β![]() ΚΆ’ΐ ΐbΚψ≥…ΝΔΘ§«σ
ΚΆ’ΐ ΐbΚψ≥…ΝΔΘ§«σ![]() ΒΡΉν–Γ÷Β.
ΒΡΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…ζΈο―–ΨΩΥυΈΣ―–ΖΔ“Μ÷÷–¬“ΏΟγΘ§‘Ύ200÷Μ–ΓΑΉ σ…μ…œΫχ––ΩΤ―–Ε‘±» Β―ιΘ§ΒΟΒΫ»γœ¬Ά≥ΦΤ ΐΨίΘΚ
Έ¥Η–»Ψ≤ΓΕΨ | Η–»Ψ≤ΓΕΨ | ΉήΦΤ | |
Έ¥ΉΔ…δ“ΏΟγ | 30 |
|
|
ΉΔ…δ“ΏΟγ | 70 |
|
|
ΉήΦΤ | 100 | 100 | 200 |
œ÷¥”Έ¥ΉΔ…δ“ΏΟγΒΡ–ΓΑΉ σ÷–»Έ»Γ1÷ΜΘ§»ΓΒΫΓΑΗ–»Ψ≤ΓΕΨΓ±ΒΡ–ΓΑΉ σΒΡΗ≈¬ ΈΣ![]() .
.
Θ®ΔώΘ©ΡήΖώ”–![]() ΒΡΑ―Έ’»œΈΣΉΔ…δ¥Υ÷÷“ΏΟγ”––ßΘΩ
ΒΡΑ―Έ’»œΈΣΉΔ…δ¥Υ÷÷“ΏΟγ”––ßΘΩ
Θ®ΔρΘ©‘ΎΈ¥ΉΔ…δ“ΏΟγ«“Έ¥Η–»Ψ≤ΓΕΨ”κΉΔ…δ“ΏΟγ«“Η–»Ψ≤ΓΕΨΒΡ–ΓΑΉ σ÷–Θ§Ζ÷±π≥ι»Γ3÷ΜΫχ––≤ΓάΐΖ÷ΈωΘ§»ΜΚσ¥”’β6÷Μ–ΓΑΉ σ÷–ΥφΜζ≥ι»Γ2÷ΜΕ‘ΉΔ…δ“ΏΟγ«ιΩωΫχ––ΚΥ ΒΘ§«σ≥ιΒΫΒΡ2÷ΜΨυ «ΉΔ…δ“ΏΟγ«“Η–»Ψ≤ΓΕΨΒΡ–ΓΑΉ σΒΡΗ≈¬ .
ΗΫΘΚ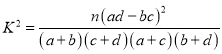 Θ§
Θ§![]() Θ§
Θ§
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com