
�ڡ�ABC�У�a��b��c�ֱ��ǽ�A��B��C�ĶԱ�,cosB�� .
.
�� ��cosA���� ,��cosC��ֵ�� ��
��AC��
,��cosC��ֵ�� ��
��AC�� ,BC��5�����ABC�����.
,BC��5�����ABC�����.
����������һ����sinB��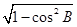 ��
�� , sinA��
, sinA�� ��
��
cosC��cos(180�㣭A��B)����cos(A��B) ��sinA.sinB��cosA��cosB
�� ��
�� ��(��
��(�� )��
)�� ��
��
�ڶ����У��� ��
�� ��
�� ��2AB��BC��cosB�� 10��
��2AB��BC��cosB�� 10�� ��25��8AB
��25��8AB
���AB��5��AB��3�ۺϵá�ABC�����Ϊ ��
��
�⣺�� sinB��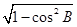 ��
�� , sinA��
, sinA�� ��
�� ,������������2��
,������������2��
��cosC��cos(180�㣭A��B)����cos(A��B) ����������������3��
��sinA.sinB��cosA��cosB ����������������4��
�� ��
�� ��(��
��(�� )��
)�� ��
�� ����������������6��
����������������6��
�� �� ��
�� ��
�� ��2AB��BC��cosB�� 10��
��2AB��BC��cosB�� 10�� ��25��8AB
������������7��
��25��8AB
������������7��
���AB��5��AB��3�� ����������������9��
��AB��5����S��ABC�� AB��BC��sinB��
AB��BC��sinB�� ��5��5��
��5��5�� ��
�� ������������10��
������������10��
��AB��3����S��ABC�� AB��BC��sinB��
AB��BC��sinB�� ��5��3��
��5��3�� ��
�� ����������������11��
����������������11��
�ۺϵá�ABC�����Ϊ ��
��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
A��
| ||||
| B��1 | ||||
C��
| ||||
D��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
. |
| m |
| C |
| 2 |
| C |
| 2 |
. |
| n |
| C |
| 2 |
| C |
| 2 |
| m |
| n |
| 1 |
| 2 |
| 11 |
| 2 |
3
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| �� |
| 6 |
| 1 |
| 2 |
| 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com