
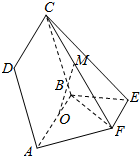
 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1分析 (Ⅰ)欲证AF⊥平面FBC,根据直线与平面垂直的判定定理可知只需证AF与平面FBC内两相交直线垂直,而BC⊥AF,BF⊥AF,BC∩BF=B,满足定理条件;
(Ⅱ)欲证OM∥平面DAF,根据直线与平面平行的判定定理可知只需证OM与平面DAF内一直线平行即可,取FD中点N,连接MN、AN,易得OM∥ON,找出了定理的条件.
解答  解:(Ⅰ)∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,
解:(Ⅰ)∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,
BC?平面ABCD,而四边形ABCD为矩形,
∴BC⊥AB,
∴BC⊥平面ABEF,
∵AF?平面ABEF,
∴BC⊥AF,
∵BF⊥AF,BC∩BF=B,
∴AF⊥平面FBC;
(Ⅱ)取FD中点N,连接MN、AN,则MN∥CD,且MN=$\frac{1}{2}$CD,
又四边形ABCD为矩形,
∴MN∥OA,且MN=OA,
∴四边形AOMN为平行四边形,
∴OM∥AN,
又∵OM?平面DAF,AN?平面DAF,
∴OM∥平面DAF.
点评 本题主要考查了直线与平面垂直的判定,以及直线与平面平行的判定,考查空间想象能力、运算求解能力、推理论证能力,考查数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{2},2]$ | B. | [2,+∞) | C. | $[\frac{1}{2},1]∪(2,+∞)$ | D. | $[\frac{1}{2},2)∪(2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 网络 | 月租费 | 本地话费 | 长途话费 |
| 甲:联通130 | 12元 | 0.36元/分 | 0.06元/秒 |
| 乙:移动“神州行” | 无 | 0.60元/分 | 0.07元/秒 |
| A. | 300秒 | B. | 400秒 | C. | 500秒 | D. | 600秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
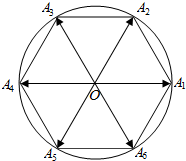 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com