
【题目】2020年冬季青奥会即将在瑞士盛大开幕,为了在射击比赛中取得优异成绩,某国拟从甲、乙两位选手中派出一位随代表团参赛,现两人进行了5次射击,射击成绩如下表(单位:分),则应派出选手及其标准差为( )
选手 次数 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
甲 | 7.4 | 8.1 | 8.6 | 8.0 | 7.9 |
乙 | 7.8 | 8.4 | 7.6 | 8.1 | 8.1 |
A.甲,0.148B.乙,0.076C.甲,![]() D.乙,
D.乙,![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知平行四边形ABCD的三个顶点的坐标为![]() ,
,![]() ,
,![]() .
.
![]() 在
在![]() 中求边AC的高线所在直线的一般方程;
中求边AC的高线所在直线的一般方程;
![]() 求平行四边形ABCD的对角线BD的长度;
求平行四边形ABCD的对角线BD的长度;
![]() 求平行四边形ABCD的面积.
求平行四边形ABCD的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,2017年国庆中秋假日期间,黔东南州共接待游客590.23万人次,实现旅游收入48.67亿元,同比分别增长44.57%、55.22%.旅游公司规定:若公司导游接待旅客,旅游年总收入不低于40(单位:百万元),则称为优秀导游.经验表明,如果公司的优秀导游率越高,则该公司的影响度越高.已知甲、乙两家旅游公司各有导游100名,统计他们一年内旅游总收入,分别得到甲公司的频率分布直方图和乙公司的频数分布表如下:

分组 |
|
|
|
|
|
频数 |
| 18 | 49 | 24 | 5 |
(Ⅰ)求![]() 的值,并比较甲、乙两家旅游公司,哪家的影响度高?
的值,并比较甲、乙两家旅游公司,哪家的影响度高?
(Ⅱ)若导游的奖金![]() (单位:万元),与其一年内旅游总收入
(单位:万元),与其一年内旅游总收入![]() (单位:百万元)之间的关系为
(单位:百万元)之间的关系为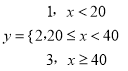 ,求甲公司导游的年平均奖金;
,求甲公司导游的年平均奖金;
(Ⅲ)从甲、乙两家公司旅游收入在![]() 的总人数中,用分层抽样的方法随机抽取6人进行表彰,其中有两名导游代表旅游行业去参加座谈,求参加座谈的导游中有乙公司导游的概率.
的总人数中,用分层抽样的方法随机抽取6人进行表彰,其中有两名导游代表旅游行业去参加座谈,求参加座谈的导游中有乙公司导游的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)是否存在一个奇数![]() ,使得数列
,使得数列![]() 中的项都在数列
中的项都在数列![]() 中?若存在,找出符合条件的一个奇数
中?若存在,找出符合条件的一个奇数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水利部门拟在黄河沿岸修建一所水库,为大致了解甲、乙两地的降水情况,随机选取汛期月份中的一周,将这一周内每日的降水量数据进行统计(单位:![]() ),制成如图所示的茎叶图.考虑以下结论:
),制成如图所示的茎叶图.考虑以下结论:
①甲地本周的平均降水量低于乙地本周的平均降水量;
②甲地本周的中位降水量高于乙地本周的平均降水量;
③甲地本周的降水量众数大于乙地本周的降水量的中位数;
④甲地本周降水量的标准差大于乙地本周降水量的标准差.

其中根据茎叶图能得到的不恰当的统计结论的编号为( )
A.①③B.②④C.①④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市化进程日益加快,劳动力日益向城市流动,某市为抽查该市内工厂的生产能力,随机抽取某个人数为1000人的工厂,其中有750人为高级工,250人为初级工,拟采用分层抽样的方法从本厂抽取100名工人,来抽查工人的生产能力,初级工和高级工的抽查结果分组情况如表1和表2.
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 |
| 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 |
| 36 | 18 |
(1)计算![]() ,
,![]() ,完成频率分直方图:
,完成频率分直方图:


图1:初级工人生产能力的频率分布直方图 图2:高级工人生产能力的频率分布直方图
(2)初级工和高级工各抽取多少人?
(3)分别估计两类工人生产能力的平均数,并估计该工厂工人生产能力的平均数.(同一组中的数据用该区间的中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 是R上的单调函数,求实数a的取值范围;
是R上的单调函数,求实数a的取值范围;
(2)设a=![]() ,
, ![]() (
(![]() ,
, ![]() ),
), ![]() 是
是![]() 的导函数.①若对任意的x>0,
的导函数.①若对任意的x>0, ![]() >0,求证:存在
>0,求证:存在![]() ,使
,使![]() <0;②若
<0;②若![]() ,求证:
,求证: ![]() <
<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然常数)时,函数
是自然常数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)当![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com