
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 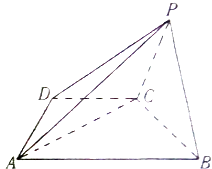
(1)求证:AC⊥PB;
(2)若PB=PC= ![]() ,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为
,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(1)证明:取AB的中点E,连结CE,
∵AB∥CD,DC= ![]() AB,∴DC
AB,∴DC ![]() AE,
AE,
∴四边形AECD是平行四边形,
又∵∠ADC=90°,∴四边形AECD是正方形,∴CE⊥AB,
∴△CAB是等腰三角开有,且CA=CB=2,AB=2 ![]() ,
,
∴AC2+CB2=AB2,∴AC⊥CB,
又∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,
∴AC⊥平面PBC,
又PB平面PBC,∴AC⊥PB

(2)解:设BC的中点为F,连结PF,
∵PB=PC,∴PF=BC,
∴PF⊥平面ABCD,∴PF⊥AC,
连结EF,则EF∥AC,∴PF⊥FE,EF⊥BC,
分别以FE、FB、FP所在的直线为x轴,y轴,z轴,建立空间直角坐标系,
∵AD=PB=PC= ![]() ,则F(0,0,0),A(2,﹣1,0),
,则F(0,0,0),A(2,﹣1,0),
B(0,1,0),D(1,﹣2,0),P(0,0,1),
∴ ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(﹣1,﹣1,0),
=(﹣1,﹣1,0), ![]() =(0,0,1),
=(0,0,1),
若在线段PB上存在一点M,设 ![]() =
= ![]() ,(0≤λ<1),
,(0≤λ<1),
∵ ![]() ,∴
,∴ ![]() =λ(0,1,﹣1)+(0,0,1)=(0,λ,1﹣λ),
=λ(0,1,﹣1)+(0,0,1)=(0,λ,1﹣λ),
∴M(0,λ,1﹣λ), ![]() ,
,
设平面MAD的一个法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,
=(1,﹣1, ![]() ),
),
平面ABCD的法向量 ![]() =(0,0,1),
=(0,0,1),
∵二面角M﹣AD﹣B的余弦值为 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
=  =
= ![]() ,
,
解得 ![]() 或λ=2(舍).
或λ=2(舍).
∴存在点M,使得二面角M﹣AD﹣B的余弦值为 ![]() ,且
,且 ![]() =
= ![]() .
.
【解析】(1)取AB的中点E,连结CE,推导出四边形AECD是正方形,从而CE⊥AB,再求出AC⊥CB,由此能证明AC⊥PB.(2)设BC的中点为F,连结PF,分别以FE、FB、FP所在的直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出结果.
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:
①D1P∥平面A1BC1;
②D1P⊥BD;
③平面PDB1⊥平面A1BC1;
④三棱锥A1﹣BPC1的体积不变.
则其中所有正确的命题的序号是_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,O为坐标原点,点
x,O为坐标原点,点![]() 在双曲线上.
在双曲线上.
(I)求双曲线C的方程.
(II)若斜率为1的直线l与双曲线交于P,Q两点,且![]() =0,求直线l方程.
=0,求直线l方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , a4+a7=20,对任意的k∈N都有Sk+1=3Sk+k2 .
(I) 求数列{an}的通项公式;
(Ⅱ)数列{bn}定义如下:2mbm(m∈N*)是使不等式an≥m成立所有n中的最小值,求{bn}的通项公式及{(﹣1)m﹣1bm}的前2m项和T2m .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x+ ![]() +1(a∈R).
+1(a∈R).
(1)讨论f(x)的单调性与极值点的个数;
(2)当a=0时,关于x的方程f(x)=m(m∈R)有2个不同的实数根x1 , x2 , 证明:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx(ω>0),将y=f(x)的图象向右平移 ![]() 个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x+y的值为( ) 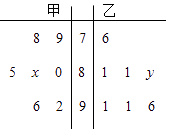
A.168
B.169
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x>0).
(x>0).
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)> ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n﹣3 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com