练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

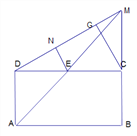
    【题目】如图①，在矩形中， ， 是的中点，将三角形沿翻折到图②的位置，使得平面 平面.

    （1）在线段上确定点，使得平面，并证明；

    （2）求与所在平面构成的锐二面角的正切值.

    【答案】(1)详见解析;(2) .

    【解析】试题分析：证明线面平行利用线面平行的判定定理，本题借助平行四边形可以得到线线平行，进而证明线面平行；求二面角一是传统方法，“一作，二证，三求”，本题采用传统方法利用线面垂直做出二面角，然后求出二面角，二是建立空间直角坐标系，借助空间向量，求法向量，利用公式求角.

    试题解析：

    (Ⅰ)点是线段中点时， 平面.

    证明：记， 的延长线交于点，因为，所以点是的中点，所以.

    而在平面内， 在平面外，所以平面.

    (Ⅱ)在矩形中， ， ，

    因为平面 平面，且交线是，所以 平面.

    在平面内作 ，连接，则 .

    所以就是与所在平面构成的锐二面角的平面角.

    因为, ，所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中为自然对数的底数），.

    （Ⅰ）当时，求的最小值；

    （Ⅱ）记，请证明下列结论：

    ①若，则对任意，有；

    ②若，则存在实数，使.

    查看答案和解析>>

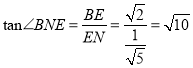    科目：高中数学 来源： 题型：

    【题目】已知二次函数g（x）=mx2﹣2mx+n+1（m＞0）在区间[0，3]上有最大值4，最小值0．
    （1）求函数g（x）的解析式；
    （2）设f（x）= ．若f（2x）﹣k2x≤0在x∈[﹣3，3]时恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，三角形ABC为等腰直角三角形，AC=BC= ，AA1=1，点D是AB的中点．
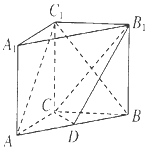
    （1）求证：AC1∥平面CDB1；
    （2）二面角B1﹣CD﹣B的平面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，已知长方形ABCD中，AB=2，AD=1，E为DC的中点．将△ADE沿AE折起，使得平面ADE⊥平面ABCE．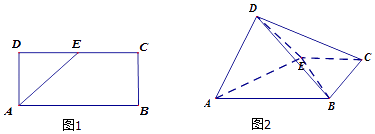
    （1）求证：平面BDE⊥平面ADE
    （2）求三棱锥 C﹣BDE的体积

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义在D上的函数y=h（x）在点P（x0 ， h（x0））处的切线方程为l：y=g（x），当x≠x0时，若 ＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”，则f（x）=x2﹣6x+4lnx的“类对称点”的横坐标是（ ）
    A.1
    B.
    C.e
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图（1）所示，已知四边形是由和直角梯形拼接而成的，其中.且点为线段的中点， ， .现将沿进行翻折，使得二面角的大小为90°，得到图形如图（2）所示，连接，点分别在线段上.

    （Ⅰ）证明： ；

    （Ⅱ）若三棱锥的体积为四棱锥体积的，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+ax，若f（f（x））的最小值与f（x）的最小值相等，则a的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约．乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约．设甲、乙、丙面试合格的概率分别是 ， ， ，且面试是否合格互不影响．求：
    （1）至少有1人面试合格的概率；
    （2）签约人数ξ的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案