Question

某数列既成等差数列也成等比数列，那么该数列一定是（ ）
A．公差为0的等差数列
B．公比为1的等比数列
C．常数数列1，1，1
D．以上都不对

Answer 1

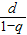
【答案】分析：先设该数列的公比为q，公差为d，则q和d均为常数，进而通过a_n+1-a_n=d化简得a_n（1-q）=d，讨论当q≠1时a_n=可推知数列{a_n}为常数列，与q≠1矛盾．进而推断q=1．答案可知．
解答：解：设该数列为{a_n}公比为q，公差为d，则q和d均为常数，
则a_n+1-a_n=a_nq-a_n=a_n（1-q）=d
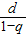
如果q≠1，则a_n=，为常数列，与q≠1矛盾．
故q必须等于1．
故选B
点评：本题主要考查了等比和等差数列性质的应用．属基础题．