
【题目】已知点![]() 在椭圆
在椭圆![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 的右顶点,点
的右顶点,点![]() 是椭圆
是椭圆![]() 上不同的两点(均异于
上不同的两点(均异于![]() )且满足直线
)且满足直线![]() 与
与![]() 斜率之积为
斜率之积为![]() .试判断直线
.试判断直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由.
是否过定点,若是,求出定点坐标,若不是,说明理由.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)由点![]() 在椭圆
在椭圆![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的方程;(2)由题意,直线
的方程;(2)由题意,直线![]() 的斜率存在,可设直线
的斜率存在,可设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,联立
,联立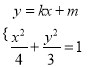 ,得
,得![]() ,根据韦达定理、斜率公式及直线
,根据韦达定理、斜率公式及直线![]() 与
与![]() 斜率之积为
斜率之积为![]() ,可得
,可得![]() ,解得
,解得![]() 或
或![]() ,将以上结论代入直线方程即可得结果.
,将以上结论代入直线方程即可得结果.
试题解析:(1)可知离心率![]() ,故有
,故有![]() ,
,
![]()
又有点![]() 在椭圆
在椭圆![]() 上,代入得
上,代入得![]() ,
,
解得![]() ,
, ![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意,直线![]() 的斜率存在,可设直线
的斜率存在,可设直线![]() 的方程为
的方程为
![]() ,
, ![]() ,
, ![]() ,
,
联立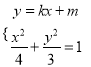 得
得![]() .
.
∴![]() ,
, ![]() .
.
∵直线![]() 与
与![]() 斜率之积为
斜率之积为![]() .
.
而点![]() ,∴
,∴![]() .
.
∴![]() .
.
化简得![]() ,
,
∴![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,直线
时,直线![]() 的方程为直线
的方程为直线![]() 与
与![]() 斜率之积为
斜率之积为![]() ,过定点
,过定点![]() .
.
![]() 代入判别式大于零中,解得
代入判别式大于零中,解得![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过定点
,过定点![]() ,不符合题意.
,不符合题意.
故直线![]() 过定点
过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2
(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2![]() cos θ.
cos θ.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .(Ⅰ)求点
.(Ⅰ)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(Ⅱ)过![]() 的直线
的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,过
两点,过![]() 作与
作与![]() 垂直的直线
垂直的直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
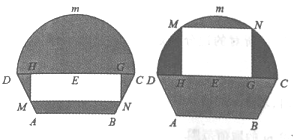
【题目】如图所示的自动通风设施.该设施的下部![]() 是等腰梯形,其中
是等腰梯形,其中![]() 为2米,梯形的高为1米,
为2米,梯形的高为1米, ![]() 为3米,上部
为3米,上部![]() 是个半圆,固定点
是个半圆,固定点![]() 为
为![]() 的中点.
的中点. ![]() 是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和
是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和![]() 平行.当
平行.当![]() 位于
位于![]() 下方和上方时,通风窗的形状均为矩形
下方和上方时,通风窗的形状均为矩形![]() (阴影部分均不通风).
(阴影部分均不通风).
(1)设![]() 与
与![]() 之间的距离为
之间的距离为![]() (
(![]() 且
且![]() )米,试将通风窗的通风面积
)米,试将通风窗的通风面积![]() (平方米)表示成关于
(平方米)表示成关于![]() 的函数
的函数![]() ;
;
(2)当![]() 与
与![]() 之间的距离为多少米时,通风窗的通风面积
之间的距离为多少米时,通风窗的通风面积![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量(![]() )”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为
)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累积净化量,以克表示.根据
时对颗粒物的累积净化量,以克表示.根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量(
《空气净化器》国家标准,对空气净化器的累计净化量(![]() )有如下等级划分:
)有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共2000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中.按照
中.按照![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:
的所有数据有: ![]() 和
和![]() ,并绘制了如下频率分布直方图:
,并绘制了如下频率分布直方图:

(1)求![]() 的值及频率分布直方图中的
的值及频率分布直方图中的![]() 值;
值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() , 若椭圆上一点
, 若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 是点
是点![]() 在
在![]() 轴上的垂足,延长
轴上的垂足,延长![]() 交椭圆
交椭圆![]() 于
于![]() ,求证:
,求证: ![]() 三点共线.
三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com