
分析 可画出图形,根据条件便有$\overrightarrow{CD}=\frac{4}{3}\overrightarrow{CB}=\frac{4}{3}\overrightarrow{AB}-\frac{4}{3}\overrightarrow{AC}$,从而便可根据平面向量基本定理得到$r=s=\frac{4}{3}$,这样便可求出s+r的值.
解答 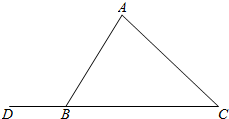 解:如图,
解:如图,
$\overrightarrow{CD}=4\overrightarrow{BD}$;
∴$\overrightarrow{CD}=\frac{4}{3}\overrightarrow{CB}=\frac{4}{3}(\overrightarrow{AB}-\overrightarrow{AC})$=$\frac{4}{3}\overrightarrow{AB}-\frac{4}{3}\overrightarrow{AC}$;
又$\overrightarrow{CD}=r\overrightarrow{AB}-s\overrightarrow{AC}$;
∴$\left\{\begin{array}{l}{r=\frac{4}{3}}\\{s=\frac{4}{3}}\end{array}\right.$;
∴$s+r=\frac{8}{3}$.
点评 考查向量数乘及向量减法的几何意义,以及向量的数乘运算,平面向量基本定理.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1) | C. | (-1,0)∪(0,1) | D. | [-1,0)∪(0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,4] | C. | [2,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1)∪(1,+∞) | C. | (0,1) | D. | (0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com