
����Ŀ��ijĦ�г�������ҵ�����������Ħ�г���Ͷ��ɱ�Ϊ1��Ԫ/����������Ϊ1.2��Ԫ/������������Ϊ1000���������Ϊ��Ӧ�г����ƻ���߲�Ʒ���Σ��ʶ�����Ͷ��ɱ�����ÿ����Ͷ��ɱ����ӵı���Ϊx��0��x��1�������������Ӧ����߱���Ϊ0.75x��ͬʱԤ�������������ӵı���Ϊ0.6x����֪������=����������Ͷ��ɱ���������������
��1��д�������Ԥ�Ƶ�������y��Ͷ��ɱ����ӵı���x�Ĺ�ϵʽ��
��2��Ϊʹ����ȵ�������������������ӣ���Ͷ��ɱ����ӵı���xӦ��ʲô��Χ�ڣ�
���𰸡���1��y=��60x2+20x+200��0��x��1������2��Ϊ��֤����ȵ��������������������ӣ�Ͷ��ɱ����ӵı���xӦ���� 0��x��![]() ��
��
��������
���⣨1��������ÿ����Ͷ��ɱ����ӵı���Ϊx��0��x��1�������������Ӧ����߱���Ϊ0.75x��ͬʱԤ�������������ӵı���Ϊ0.6x��������=����������Ͷ��ɱ�����������������������ģ�ͣ�Ҫע�ⶨ����
��2��Ҫ��֤����ȵ������������������ӣ�ֻ�����������ȥ����������㼴�ɣ��ⲻ��ʽ����ý����Ҫע������ķ�Χ��
�⣺��1���������
y=[1.2����1+0.75x����1����1+x��]��1000����1+0.6x����0��x��1����4�֣�
������y=��60x2+20x+200��0��x��1������6�֣�
��2��Ҫ��֤����ȵ������������������ӣ����ҽ���![]()
��![]() ��9�֣�
��9�֣�
�ⲻ��ʽ��![]() ��
��
��Ϊ��֤����ȵ��������������������ӣ�Ͷ��ɱ����ӵı���xӦ���� 0��x��![]() ����12�֣�
����12�֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��������������
��������������![]() ������
������![]() ��
��![]() ���е�
���е�![]() Ϊ��������������
��������������![]() ������
������![]() ��
��![]() ���е�
���е�![]() Ϊ��������������
��������������![]() ��
��![]() ����˼�����ȥ.�����½��ۣ�
����˼�����ȥ.�����½��ۣ�

���������������εı߳����ɹ���Ϊ![]() �ĵȱ����У�
�ĵȱ����У�
��ÿһ���������ζ���һ��������ֱ��![]() �ϣ�
�ϣ�
�۵������������εIJ��ڵ�����������α��ϵĶ���![]() ��������
��������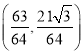 ��
��
�ܵ�![]() ���������εIJ��ڵ�
���������εIJ��ڵ�![]() ���������α��ϵĶ���
���������α��ϵĶ���![]() �ĺ�������
�������![]() ����
����![]() .
.
������ȷ���۵������___________.��������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ��Ϊ
��Բ��Ϊ![]() ����
����![]() ��Բ
��Բ![]() ��һ�����㣬��
��һ�����㣬��![]() ��Բ
��Բ![]() ������һ�㣬�߶�
������һ�㣬�߶�![]() ����ֱƽ������뾶
����ֱƽ������뾶![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
��1����![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��2��������![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ��켣
��켣![]() �ཻ��
�ཻ��![]() ���㣨����ͬ�ڵ�
���㣨����ͬ�ڵ�![]() ����֤����ֱ��
����֤����ֱ��![]() ��ֱ��
��ֱ��![]() ��б��֮��Ϊ��ֵ��
��б��֮��Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��![]() 1��a��b��0�������ҽ���ֱ�ΪF1��F2����P����1��
1��a��b��0�������ҽ���ֱ�ΪF1��F2����P����1��![]() ������ԲC�ϣ���|PF2|
������ԲC�ϣ���|PF2|![]() ��
��
��1������ԲC�ķ��̣�
��2������F2��ֱ��l����ԲC����A��B���㣬MΪ�߶�AB���е㣬����ԲC�ϴ��ڵ�N������![]() 3
3![]() ��OΪ����ԭ�㣩����ֱ��l�ķ��̣�
��OΪ����ԭ�㣩����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ������
������![]() ������
������
��1��֤���� ![]() ��
��
��2���Ƿ����![]() ��ʹ��
��ʹ��![]() Ϊ�Ȳ����У���˵�����ɣ�
Ϊ�Ȳ����У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC:![]() l(a>b>0)������(
l(a>b>0)������(![]() ,1),��������e
,1),��������e![]() .
.
(1)����ԲC�ķ���;
(2)��ֱ��l����ԲC�ཻ��AB����,�������AOB=90��(OΪ����ԭ��),��|AB|��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˽���Χ�����������Ҫ��˫�����������壬��ʼʱ��ÿ����Ӯ�ĸ���Ϊ![]() ��������̬���ȣ���һ����һ���壬�����ÿ����Ӯ�ĸ��ʾͱ�Ϊ
��������̬���ȣ���һ����һ���壬�����ÿ����Ӯ�ĸ��ʾͱ�Ϊ![]() ���������û�к��壬����֪ǰ�����嶼�Ǽ�Ӯ��
���������û�к��壬����֪ǰ�����嶼�Ǽ�Ӯ��
��������������Ӯ�ĸ��ʣ�
�������������ʱ����ǡ��Ӯ������ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com