解:(1)由题意可得

=(sinα-1)+(1-cosα)=sinα-cosα=

①,且α为锐角.
平方可得1-2sinαcosα=

,即sin2α=

②.
由①②解得 sinα=

,cosα=

.
(2)∵函数f(x)=5cos(2x-α)+cos2x=5cos2xcosα+5sin2xsinα+cos2x=4sin2x+4cos2x
=4

sin(2x+

),
故函数f(x)的最小正周期为

=π.
令2x+

=kπ,k∈z,可得x=
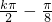
,故对称中心的坐标为(
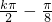
,0),k∈z.
(3)由于当x∈
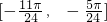
时,(2x+

)∈[-

,-

],
故-1≤sin(2x+

)≤-

,-4

≤4

sin(2x+

)≤-2

,
故函数f(x)的值域为[-4

,-2

].
分析:(1)由题意可得

=sinα-cosα=

①,且α为锐角,平方可得sin2α=

②,解①②可得sinα,cosα的值.
(2)利用三角函数的恒等变换化简函数f(x)的解析式为4

sin(2x+

),由此求得最小正周期,以及对称中心的坐标
(3)由于当x∈
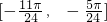
时,(2x+

)∈[-

,-

],由此求得sin(2x+

) 的范围,即可求得函数f(x)的值域.
点评:本题主要考查两个向量的数量积公式的应用,三角函数的恒等变换及化简求值,复合三角函数的对称性、定义域和值域,属于中档题.

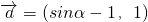 ,
,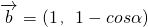 ,
, •
• =
= ,α∈(0,
,α∈(0, ).
).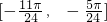 上的值域.
上的值域. =(sinα-1)+(1-cosα)=sinα-cosα=
=(sinα-1)+(1-cosα)=sinα-cosα= ①,且α为锐角.
①,且α为锐角. ,即sin2α=
,即sin2α= ②.
②. ,cosα=
,cosα= .
. sin(2x+
sin(2x+ ),
), =π.
=π. =kπ,k∈z,可得x=
=kπ,k∈z,可得x=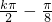 ,故对称中心的坐标为(
,故对称中心的坐标为(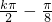 ,0),k∈z.
,0),k∈z.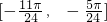 时,(2x+
时,(2x+ )∈[-
)∈[- ,-
,- ],
], )≤-
)≤- ,-4
,-4  ≤4
≤4 sin(2x+
sin(2x+ )≤-2
)≤-2 ,
, ,-2
,-2 ].
]. =sinα-cosα=
=sinα-cosα= ①,且α为锐角,平方可得sin2α=
①,且α为锐角,平方可得sin2α= ②,解①②可得sinα,cosα的值.
②,解①②可得sinα,cosα的值. sin(2x+
sin(2x+ ),由此求得最小正周期,以及对称中心的坐标
),由此求得最小正周期,以及对称中心的坐标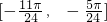 时,(2x+
时,(2x+ )∈[-
)∈[- ,-
,- ],由此求得sin(2x+
],由此求得sin(2x+ ) 的范围,即可求得函数f(x)的值域.
) 的范围,即可求得函数f(x)的值域.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案