练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知等比数列{an}中，a1，a13是方程x2-8x+1=0的两个根，则a5•a7•a9等于（　　）
    A、1或-1B、-1C、1D、2
    考点：等比数列的性质,等比关系的确定
    专题：等差数列与等比数列
    分析：等比数列an中a7是a1，a13的等比中项，由此可以利用根与系数的关系求出两根之积，即得出a7的平方，再由a1，a13的和为正数确定出a7的符号．然后求解a5•a7•a9的值．
    解答： 解：由题意a1，a13是方程x2-8x+1=0的两个根
    ∴a1a13=1，a1+a13=8
    又等比数列an中，可得数列的所有的奇数项都是正项，
    故可得a7=1，
    a5•a7•a9=a73=1
    故选：C．
    点评：本题考查等比数列的性质，解题的关键是熟练掌握等比数列的性质，且能根据这些性质灵活变形与求值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设a=20.3，b=log
    		2
    3，c=ln（ln2）则（　　）
    A、a＞b＞c
    B、a＞c＞b
    C、b＞a＞c
    D、b＞c＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设集合A={x|-1＜x＜3}，集合B={x|x≥1}，则A∩B=（　　）
    A、{x|1＜x＜3}
    B、{x|1≤x＜3}
    C、{x|1＜x≤3}
    D、{x|1≤x≤3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，A、B、C的对边分别是a、b、c，且c2=bccosA+cacosB+abcosC，则△ABC的形状为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    2014年11月12日，科幻巨片《星际穿越》上映，上映至今，全球累计票房高达6亿美金．为了解绵阳观众的满意度，某影院随机调查了本市观看此影片的观众，并用“10分制”对满意度进行评分，分数越高满意度越高，若分数不低于9分，则称该观众为“满意观众”．现从调查人群中随机抽取12名，如果所示的茎叶图记录了他们的满意度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）．
    （1）求从这12人中随机选取2人，至少有1人为“满意观众”的概率；
    （2）一本次抽样的频率作为概率，从整个绵阳市观看此影片的观众中任选3人，记ξ表示抽到“满意观众”的人数，求ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设F1、F2分别为双曲线
    x2
    a2
    -
    y2
    b2
    =1    （a、b＞0）的左、右焦点，过F2的直线交双曲线的右支于A、B两点，设△AF1F2和△BF1F2的内心分别为C、D．若 当|CD|=
    9a
    4
    时，直线AB的倾斜角的正弦为
    8
    9
    ．则双曲线的离心率为（　　）
    A、
    		2
    B、2
    C、3
    D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知
    a
    =（1，2），
    b
    =（-2，1），则
    a
    与
    b
    （　　）
    A、垂直B、不垂直也不平行
    C、平行且反向D、平行且同向

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=
    		x+3
    +
    1
    x+2
    的定义域是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

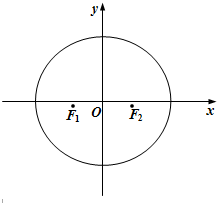    如图所示，已知椭圆C的两个焦点分别为F1（-1，0）、F2（1，0），且F2到直线x-
    		3
    y-9=0的距离等于椭圆的短轴长．
    （Ⅰ） 求椭圆C的方程；
    （Ⅱ） 若圆P的圆心为P（0，t）（t＞0），且经过F1、F2，Q是椭圆C上的动点且在圆P外，过Q作圆P的切线，切点为M，当|QM|的最大值为
    3
    		2
    2
    时，求t的值．

    查看答案和解析>>

    同步练习册答案