考点:函数恒成立问题,函数的最值及其几何意义
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)运用偶函数的定义和一次函数的解析式,即可得到a,b,c;
(Ⅱ)令x=1,则a+b+c=2,再由二次不等式恒成立,结合抛物线开口向上,且判别式不大于0,即可得到a的范围,进而得到所求范围;
(Ⅲ)对任意x1,x2∈[-1,1]都有|f2(x1)-f2(x2)|≤4等价于在[-1,1]上的最大值与最小值之差M≤4,对b讨论,分b>2时,0<b≤2时,-2≤b≤0时,分别求出最大值和最小值,计算即可得到.
解答:
解:(Ⅰ)由 f
1(x)=3x+1,f
2(x)为偶函数得
∴a=3,b=0,c=1;
(Ⅱ)由题意可知f
2(1)≥2,f
2(1)≤2,
∴f
2(1)=2,∴a+b+c=2,
∵对任意实数x都有f
2(x)≥2x,即ax
2+(b-2)x+c≥0恒成立,
∴
,由a+b+c=2,∴(a+c)
2-4ac≤0,
可得a=c,b=2-2a,
此时
f2(x)-(x+1)2=(a-)(x-1)2,
∵对任意实数x都有
f2(x)≤(x+1)2成立,∴
0<a≤,
∴f
2(-1)=a-b+c=4a-2的取值范围是(-2,0];
(Ⅲ)对任意x
1,x
2∈[-1,1]都有|f
2(x
1)-f
2(x
2)|≤4等价于
在[-1,1]上的最大值与最小值之差M≤4,据此分类讨论如下:
(ⅰ)当
||>1,即b>2时,M=|f
2(1)-f
2(-1)|=2|b|>4,与题设矛盾.
(ⅱ) 当
-1≤-<0,即0<b≤2时,
M=f2(1)-f2(-)=(+1)2≤4恒成立.
(ⅲ)当
0≤-<1,即-2≤b≤0时,
M=f2(-1)-f2(-)=(-1)2≤4恒成立.
综上可知,-2≤b≤2.
点评:本题考查函数的奇偶性和单调性的运用,考查二次不等式的恒成立问题,注意运用图象和判别式的符号,考查函数的最值,考查分类讨论的思想方法,属于中档题和易错题.



 导学教程高中新课标系列答案
导学教程高中新课标系列答案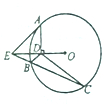 如图,AE是的⊙O切线,A是切点,AD⊥OE于点D,割线EC交⊙O于B,C两点.
如图,AE是的⊙O切线,A是切点,AD⊥OE于点D,割线EC交⊙O于B,C两点.