
【题目】如图,在多面体EF﹣ABCD中,ABCD,ABEF均为直角梯形, ![]() ,DCEF为平行四边形,平面DCEF⊥平面ABCD.
,DCEF为平行四边形,平面DCEF⊥平面ABCD. 
(1)求证:DF⊥平面ABCD;
(2)若△ABD是等边三角形,且BF与平面DCEF所成角的正切值为 ![]() ,求二面角A﹣BF﹣C的平面角的余弦值.
,求二面角A﹣BF﹣C的平面角的余弦值.
【答案】
(1)证明:因为 ![]() ,所以AB⊥平面BCE,
,所以AB⊥平面BCE,
又EF∥CD,所以EF∥平面ABCD,从而有AB∥CD∥EF,
所以CD⊥平面BCE,从而CD⊥CE,
又CE∥DF,所以CD⊥DF,
又平面DCEF⊥平面ABCD,所以DF⊥平面ABCD.
(2)解法1:过C作CH⊥BE交BE于H,HK⊥BF交BF于K,
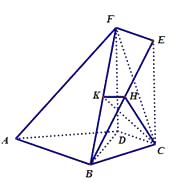
因为AB⊥平面BCE,所以CH⊥AB,从而CH⊥平面ABEF,
所以CH⊥BF,从而BF⊥平面CHK,所以BF⊥KH
即∠HKC为C﹣BF﹣E的平面角,与 A﹣BF﹣C的平面角互补.
因为BC⊥DCEF,所以BF与平面DCEF所成角为∠BFC.
由 ![]() ,所以2CB2=CD2+CE2,
,所以2CB2=CD2+CE2,
由△ABD是等边三角形,知∠CBD=30°,所以 ![]()
令CD=a,所以 ![]() ,
, ![]() .
.
所以 ![]() ,
, ![]() .
.
所以二面角A﹣BF﹣C的平面角的余弦值为 ![]() .
.
解法2:因为CB,CD,CE两两垂直,
以C为原点,CD,CB,CE所在直线为x,y,z轴,如图建立空间直角坐标系.
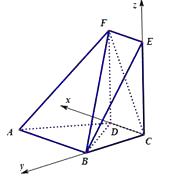
不妨设CD=1.
因为BC⊥DCEF,所以BF与平面DCEF所成角为∠BFC.
由 ![]() ,所以2CB2=CD2+CE2,
,所以2CB2=CD2+CE2,
由△ABD是等边三角形,知∠CBD=30°,
所以 ![]() ,
,
![]()
![]() ,
, ![]()
平面ABF的一个法向量 ![]() ,平面CBF的一个法向量
,平面CBF的一个法向量 ![]()
则 ![]() ,且
,且 ![]()
取 ![]()
则 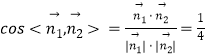 .
.
二面角A﹣BF﹣C的平面角与 ![]() 的夹角互补.
的夹角互补.
所以二面角A﹣BF﹣C的平面角的余弦值为 ![]() .
.
【解析】(1)推导出AB⊥平面BCE,AB∥CD∥EF,从而CD⊥平面BCE,进而CD⊥CE,由CE∥DF,得CD⊥DF,由此能证明DF⊥平面ABCD.(2)法1:过C作CH⊥BE交BE于H,HK⊥BF交BF于K,推导出∠HKC为C﹣BF﹣E的平面角,由此能求出二面角A﹣BF﹣C的平面角的余弦值.法2:以C为原点,CD,CB,CE所在直线为x,y,z轴,建立空间直角坐标系.不妨设CD=1,利用向量法能求出二面角A﹣BF﹣C的平面角的余弦值.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】(2015·北京)某校老年、中年和青年教师的人数见下表,采用分层抽样的方法调查教师的身体状况,在抽取的样本
中,青年教师有320人,则该样本的老年教师人数为( )
A.90
B.100
C.180
D.300
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是双曲线C: ![]() =1(a>0,b>0)的左、右焦点,其离心率为e,点B的坐标为(0,b),直线F1B与双曲线C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴,直线F1B的交点分别为M,R,若△RMF1与△PQF2的面积之比为e,则双曲线C的离心率为( )
=1(a>0,b>0)的左、右焦点,其离心率为e,点B的坐标为(0,b),直线F1B与双曲线C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴,直线F1B的交点分别为M,R,若△RMF1与△PQF2的面积之比为e,则双曲线C的离心率为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A1 , A2 , …,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为: ![]() .则下列说法中,错误的是( )
.则下列说法中,错误的是( ) 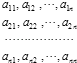
A.数阵中第一列的数全是0当且仅当A1=
B.数阵中第n列的数全是1当且仅当An=S
C.数阵中第j行的数字和表明集合Aj含有几个元素
D.数阵中所有的n2个数字之和不超过n2﹣n+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义运算: ![]() =a1a4﹣a2a3 , 将函数f(x)=
=a1a4﹣a2a3 , 将函数f(x)= ![]() (ω>0)的图象向左平移
(ω>0)的图象向左平移 ![]() 个单位,所得图象对应的函数为偶函数,则ω的最小值是( )
个单位,所得图象对应的函数为偶函数,则ω的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=92n﹣1 , n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=(n﹣1)an , 数列{bn}的前n项和为Sn , 若不等式Sn>kan+16n﹣26对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲抛掷均匀硬币2017次,乙抛掷均匀硬币2016次,下列四个随机事件的概率是0.5的是( )
①甲抛出正面次数比乙抛出正面次数多;
②甲抛出反面次数比乙抛出正面次数少;
③甲抛出反面次数比甲抛出正面次数多;
④乙抛出正面次数与乙抛出反面次数一样多.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com