
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】在底面是菱形的四棱锥![]() 中,
中,![]() .
.
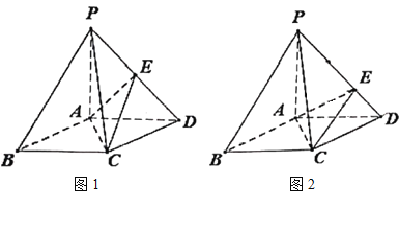
(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上.
上.
①如图1,若点![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
②如图2,若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为维护交通秩序,防范电动自行车被盗,天津市公安局决定,开展二轮电动自行车免费登记、上牌照工作.电动自行车牌照分免费和收费(安装防盗装置)两大类,群众可以 自愿选择安装.已知甲、乙、丙三个不同类型小区的人数分别为15000,15000,20000.交管部门为了解社区居民意愿,现采用分层抽样的方法从中抽取10人进行电话访谈.
(Ⅰ)应从甲小区和丙小区的居民中分别抽取多少人?
(Ⅱ)设从甲小区抽取的居民为![]() ,丙小区抽取的居民为
,丙小区抽取的居民为![]() .现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
.现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
(ⅰ)试用所给字母列举出所有可能的抽取结果;
(ⅱ)设![]() 为事件“抽取的2人来自不同的小区”,求事件
为事件“抽取的2人来自不同的小区”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).

某市随机抽取10户同一个月的用电情况,得到统计表如下:

(1)若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯每度0.8元,试计算![]() 居民用电户用电410度时应交电费多少元?
居民用电户用电410度时应交电费多少元?
(2)现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
(3)以表中抽到的10户作为样本估计全市居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水.已知该厂生活用水为每小时10吨,生产用水量![]() (吨)与时间
(吨)与时间![]() (单位:小时,且规定早上6时
(单位:小时,且规定早上6时![]() )的函数关系式为:
)的函数关系式为:![]() ,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
(1)若进水量选择为![]() 级,水塔中剩余水量为
级,水塔中剩余水量为![]() 吨,试写出
吨,试写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如何选择进水量,既能始终保证该厂的用水(水塔中水不空)又不会使水溢出?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)求函数![]() 的定义域,并求出当
的定义域,并求出当![]() 时,常数
时,常数![]() 的值;
的值;
(2)在(1)的条件下,判断函数![]() 在
在![]() 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)设![]() ,若方程
,若方程![]() 有实根,求
有实根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com