
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC=![]() BC=1,E是PC的中点,平面PAC⊥平面ABCD.
BC=1,E是PC的中点,平面PAC⊥平面ABCD.

(1)证明:ED∥平面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
【答案】
【解析】(1)如图,取PB的中点F,连接AF,![]() .
.
∵EF是![]() 的中位线,∴EF∥BC,且EF=
的中位线,∴EF∥BC,且EF=![]() .(2分)
.(2分)
又![]() ,且AD=
,且AD=![]() ,∴AD∥EF且AD=EF,则四边形ADEF是平行四边形.
,∴AD∥EF且AD=EF,则四边形ADEF是平行四边形.
∴DE∥AF,又DE平面ABP,AF平面ABP,∴ED∥平面PAB.(5分)
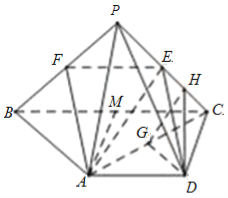
(2)如图,取BC的中点M,连接AM,则AD∥MC且AD=MC,∴四边形ADCM是平行四边形,
∴AM=MC=MB,则A在以BC为直径的圆上,∴AB⊥AC,可得![]() .
.
过D作DG⊥AC于G,∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴DG⊥平面PAC,则DG⊥PC.
过G作![]() 于
于![]() ,则PC⊥平面GHD,连接DH,则PC⊥DH,
,则PC⊥平面GHD,连接DH,则PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.(9分)
在![]() 中,
中,![]() ,连接AE,
,连接AE,![]() .
.
在![]() 中,
中,![]() ,则
,则![]() .
.
即二面角A﹣PC﹣D的余弦值为![]() .(12分)
.(12分)


科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等式:sin25°+cos235°+sin 5°cos 35°=![]() ,
,
sin215°+cos245°+sin 15°cos 45°=![]() ,sin230°+cos260°+sin 30°·cos 60°=
,sin230°+cos260°+sin 30°·cos 60°=![]() ,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4![]() 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,在以原点
,在以原点![]() 为极点,
为极点, ![]() 轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为
轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线![]() 与曲线C有公共点,求
与曲线C有公共点,求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() 为曲线C上任意一点,求
为曲线C上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若BA,求实数m的取值范围;
(2)当x∈R时,不存在元素x使x∈A与x∈B同时成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,海上有![]() 、
、![]() 两个小岛相距
两个小岛相距![]() ,船
,船![]() 将保持观望
将保持观望![]() 岛和
岛和![]() 岛所成的视角为
岛所成的视角为![]() ,现从船
,现从船![]() 上派下一只小艇沿
上派下一只小艇沿![]() 方向驶至
方向驶至![]() 处进行作业,且
处进行作业,且![]() .设
.设![]() .
.

(1)用![]() 分别表示
分别表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)0晚上小艇在![]() 处发出一道强烈的光线照射
处发出一道强烈的光线照射![]() 岛,
岛,![]() 岛至光线
岛至光线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为(-1,1),满足f(-x)=-f(x),且
的定义域为(-1,1),满足f(-x)=-f(x),且![]() .
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(-1,1)上是增函数;
(3)解不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com