
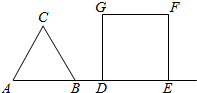
 如图所示,A、B、D、E四点在同一直线上,△ABC是边长为2的正三角形,DEFG是边长为2的正方形,在静止状态时,B点在D点的左侧,且$|{\overrightarrow{BD}}|=1$,让A点沿直线AB从左到右运动,当A点运动到E点时,运动结束.
如图所示,A、B、D、E四点在同一直线上,△ABC是边长为2的正三角形,DEFG是边长为2的正方形,在静止状态时,B点在D点的左侧,且$|{\overrightarrow{BD}}|=1$,让A点沿直线AB从左到右运动,当A点运动到E点时,运动结束.分析 (1)在静止状态时,以D为原点建立如图所示直角坐标系,用坐标表示向量,再利用向量的数量积公式,即可求在静止状态时,$\overrightarrow{BF}•\overrightarrow{CE}$的值;
(2)当A点运动时,用坐标表示向量,再利用向量的数量积公式,即可求求$\overrightarrow{BF}•\overrightarrow{CE}$的最小值.
解答  解:(1)在静止状态时,以D为原点建立如图所示直角坐标系,依题意得
解:(1)在静止状态时,以D为原点建立如图所示直角坐标系,依题意得
$\overrightarrow{BF}$=(3,2),$\overrightarrow{CE}$=(4,-$\sqrt{3}$),则
$\overrightarrow{BF}•\overrightarrow{CE}$=12-2$\sqrt{3}$…(6分)
(2)在运动状态时,仍然如上图建立直角坐标系,
设A(m,0),依题意得-3≤m≤2,
这时$\overrightarrow{BF}$=(-m,2),$\overrightarrow{CE}$=(1-m,-$\sqrt{3}$),…(10分)
则$\overrightarrow{BF}•\overrightarrow{CE}$=m2-m-2$\sqrt{3}$=(m-$\frac{1}{2}$)2-2$\sqrt{3}$-$\frac{1}{4}$
由-3≤m≤2知,当m=$\frac{1}{2}$时,$\overrightarrow{BF}•\overrightarrow{CE}$的值最小,且最小值为-2$\sqrt{3}$-$\frac{1}{4}$.…(15分)
点评 本题考查向量知识的运用,考查配方法,正确建立坐标系是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为迎接茶博会,要设计如图的一张矩形广告,该广告含有带下相等的左中右三个矩形栏目,这三栏的面积之比为60000cm2,四周空白的宽度为10cm,栏与栏之间的中缝空白的宽度为值5cm,怎样确定栏目的高与宽之比,能使整个矩形广告面积最小.
为迎接茶博会,要设计如图的一张矩形广告,该广告含有带下相等的左中右三个矩形栏目,这三栏的面积之比为60000cm2,四周空白的宽度为10cm,栏与栏之间的中缝空白的宽度为值5cm,怎样确定栏目的高与宽之比,能使整个矩形广告面积最小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab的最大值为$\frac{1}{8}$ | B. | $\frac{1}{ab}$的最小值为8 | ||
| C. | a2+ab+b2的最小值为$\frac{1}{4}$ | D. | $\frac{1}{{{a^2}+ab+{b^2}}}$的最大值为4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$.
已知函数$f(x)=\left\{\begin{array}{l}x+2{\;}^{\;}(x<0)\\{x^2}{\;}^{\;}{\;}^{\;}(0≤x<2)\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}(x≥2)\end{array}\right.$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com