
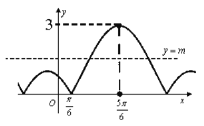
【题目】如图是函数![]() 的部分图象.
的部分图象.

(1)求函数![]() 的表达式;
的表达式;
(2)若函数![]() 满足方程
满足方程![]() ,求在
,求在![]() 内的所有实数根之和;
内的所有实数根之和;
(3)把函数![]() 的图象的周期扩大为原来的两倍,然后向右平移
的图象的周期扩大为原来的两倍,然后向右平移![]() 个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数
个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数![]() 的图象.若对任意的
的图象.若对任意的![]() ,方程
,方程![]() 在区间
在区间![]() 上至多有一个解,求正数
上至多有一个解,求正数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)答案不唯一,具体见解析(3)
(2)答案不唯一,具体见解析(3)![]()
【解析】
(1)根据图像先确定A,再确定![]() ,代入一个特殊点再确定
,代入一个特殊点再确定![]() 。
。
(2)根据(1)的结果结合图像即可解决。
(3)根据(1)的结果以及三角函数的变换求出![]() 即可解决。
即可解决。
解:(Ⅰ)由图可知:![]() ,即
,即![]() ,
,
![]() 又由图可知:
又由图可知:![]() 是五点作图法中的第三点,
是五点作图法中的第三点,
![]() ,即
,即![]() .
.
(Ⅱ)因为![]() 的周期为
的周期为![]() ,
,![]() 在
在![]() 内恰有
内恰有![]() 个周期.
个周期.
⑴当![]() 时,方程
时,方程![]() 在
在![]() 内有
内有![]() 个实根,
个实根,
设为![]()
![]() ,结合图像知
,结合图像知![]()
![]() ,
,
故所有实数根之和为![]() ;
;
⑵当![]() 时,方程
时,方程![]() 在
在![]() 内有
内有![]() 个实根为
个实根为![]() ,
,
故所有实数根之和为![]() ;
;
⑶当![]() 时,方程
时,方程![]() 在
在![]() 内有
内有![]() 个实根,
个实根,
设为![]()
![]() ,结合图像知
,结合图像知![]()
![]() ,
,
故所有实数根之和为![]() ;
;
综上:当![]() 时,方程
时,方程![]() 所有实数根之和为
所有实数根之和为![]() ;
;
当![]() 时,方程
时,方程![]() 所有实数根之和为
所有实数根之和为![]() ;
;
(Ⅲ)![]() ,
,
函数![]() 的图象如图所示:
的图象如图所示:
则当![]() 图象伸长为原来的
图象伸长为原来的![]() 倍以上时符合题意,
倍以上时符合题意,
所以![]() .
.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知点P1(a1 , b1),P2(a2 , b2),…,Pn(an , bn)(n∈N*)都在函数y=![]() 的图象上.
的图象上.
(Ⅰ)若数列{bn}是等差数列,求证数列{an}为等比数列;
(Ⅱ)若数列{an}的前n项和为Sn=1﹣2﹣n , 过点Pn , Pn+1的直线与两坐标轴所围成三角形面积为cn , 求使cn≤t对n∈N*恒成立的实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 处有一港口,两艘海轮
处有一港口,两艘海轮![]() 同时从港口
同时从港口![]() 处出发向正北方向匀速航行,海轮
处出发向正北方向匀速航行,海轮![]() 的航行速度为20海里/小时,海轮
的航行速度为20海里/小时,海轮![]() 的航行速度大于海轮
的航行速度大于海轮![]() .在港口
.在港口![]() 北偏东60°方向上的
北偏东60°方向上的![]() 处有一观测站,1小时后在
处有一观测站,1小时后在![]() 处测得与海轮
处测得与海轮![]() 的距离为30海里,且
的距离为30海里,且![]() 处对两艘海轮
处对两艘海轮![]() ,
,![]() 的视角为30°.
的视角为30°.

(1)求观测站![]() 到港口
到港口![]() 的距离;
的距离;
(2)求海轮![]() 的航行速度.
的航行速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】使用支付宝和微信支付已经成为广大消费者最主要的消费支付方式,某超市通过统计发现一周内超市每天的净利润![]() (万元)与每天使用支付宝和微信支付的人数
(万元)与每天使用支付宝和微信支付的人数![]() (千人)具有线性相关关系,并得到最近一周
(千人)具有线性相关关系,并得到最近一周![]() 的7组数据如下表,并依此作为决策依据.
的7组数据如下表,并依此作为决策依据.

(1)作出散点图,并求出回归方程![]() (
(![]() ,
,![]() 精确到
精确到![]() );
);

(2)超市为了刺激周一消费,拟在周一开展使用支付宝和微信支付随机抽奖活动,总奖金7万元.根据市场调查,抽奖活动能使使用支付宝和微信支付消费人数增加7千人,试决策超市是否有必要开
展抽奖活动?
(3)超市管理层决定:从周一到周日,若第二天的净利润比前一天增长超过两成,则对全体员工进行奖励,在(Ⅱ)的决策下,求全体员工连续两天获得奖励的概率.
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.

(1)求![]() 的值;
的值;
(2)分别求出甲、乙两组数据的方差![]() 和
和![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市通过随机询问100名不同年级的学生是否能做到“扶跌倒老人”,得到如下列联表:
做不到 | 能做到 | |
高年级 | 45 | 10 |
低年级 | 30 | 15 |
则下列结论正确的是( )
附参照表:
| 0.10 | 0.025 | 0.01 |
| 2.706 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]()
A. 在犯错误的概率不超过![]() 的前提下,认为“学生能否做到‘扶跌倒老人’与年级高低有关”
的前提下,认为“学生能否做到‘扶跌倒老人’与年级高低有关”
B. 在犯错误的概率不超过![]() 的前提下,“学生能否做到‘扶跌倒老人’与年级高低无关”
的前提下,“学生能否做到‘扶跌倒老人’与年级高低无关”
C. 有![]() 以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低有关”
以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低有关”
D. 有![]() 以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低无关”
以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知命题![]() :实数
:实数![]() 满足
满足![]() ,命题
,命题![]() :实数
:实数![]() 满足方程
满足方程![]() 表示的焦点在
表示的焦点在![]() 轴上的椭圆,且
轴上的椭圆,且![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围;
的取值范围;
(2)设命题![]() :关于
:关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ;
;![]() :函数
:函数![]() 的定义域为
的定义域为![]() .若
.若![]() 是真命题,
是真命题,![]() 是假命题,求实数
是假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com