
分析 (1)ξ的所有可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
(2)设“从6个题库中任意取出2个题库,恰好取到一个新题库”为事件B,则“2017年时恰好取到一个新题库”就是事件A0B,由此能求出2017年期末考试时恰好到1个新题库的概率.
解答 (本小题满分12分)
解:(1)ξ的所有可能取值为0,1,2,
设“2016年期末考试时取到i个新题库(即ξ=i)”为事件Ai(i=0,1,2).
又因为6个题库中,其中3个是新题库,3个是旧题库,
所以$P({A_0})=P(ξ=0)=\frac{C_3^2}{C_6^2}=\frac{1}{5}$;$P({A_1})=P(ξ=1)=\frac{C_3^1C_3^1}{C_6^2}=\frac{3}{5}$;$P({A_2})=P(ξ=2)=\frac{C_3^2}{C_6^2}=\frac{1}{5}$,
所以ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | -67 | C. | 1313 | D. | -6767 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
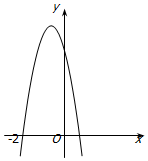 已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.
已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f'(x)的图象经过点(-2,0),如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 由a的取值确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .$1+\sqrt{5}$ | B. | .$1-\sqrt{5}$ | C. | $.1±\sqrt{5}$ | D. | .$-1-\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 理科 | 文科 | |
| 男 | 14 | 10 |
| 女 | 6 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | 0 | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com