
【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB= ![]() ,EF=1,BC=
,EF=1,BC= ![]() ,且M是BD的中点..
,且M是BD的中点.. 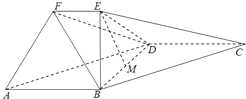
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
【答案】
(1)解:取AD的中点N,连接MN,NF.
在△DAB中,M是BD的中点,N是AD的中点,
∴MN∥AB,MN= ![]() AB.
AB.
又∵EF∥AB,EF= ![]() AB,∴MN∥EF且MN=EF,
AB,∴MN∥EF且MN=EF,
∴四边形MNFE为平行四边形,可得EM∥FN.
又∵FN平面ADF,EM平面ADF,
∴EM∥平面ADF;
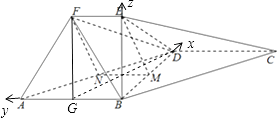
(2)解:取AB中点G,连接FG,DG,则FG∥EB,FG= ![]()
∵EB⊥平面ABCD,∴FG⊥平面ABCD,
∴∠FDG为直线DF和平面ABCD所成角
∵BC= ![]() ,AB=2,∠ABD=90°,∴BD=3
,AB=2,∠ABD=90°,∴BD=3
∵BG=1,∴DG= ![]()
∴tan∠FDG= ![]() =
= ![]() =
= ![]()
(3)解:因为EB⊥平面ABD,AB⊥BD,故以B为原点,建立空间直角坐标系B﹣xyz.
由已知可得B(0,0,0),A(0,2,0),D(3,0,0),F(0,1, ![]() )
)
∴ ![]() =(3,﹣2,0),
=(3,﹣2,0), ![]() =(0,﹣1,
=(0,﹣1, ![]() ).
).
设平面ADF的一个法向量是 ![]() =(x,y,z).
=(x,y,z).
由 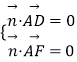 ,得
,得 ![]() ,令y=3,则
,令y=3,则 ![]() =(2,3,
=(2,3, ![]() )
)
因为EB⊥平面ABD,所以EB⊥BD.
又因为AB⊥BD,所以BD⊥平面EBAF.
∴ ![]() =(3,0,0)是平面EBAF的一个法向量.
=(3,0,0)是平面EBAF的一个法向量.
∴cos< ![]() >=
>= ![]() =
= ![]()
∵二面角D﹣AF﹣B为锐角,
∴二面角D﹣AF﹣B的大小为60°
【解析】(1)取AD的中点N,连接MN、NF.由三角形中位线定理,结合已知条件,证出四边形MNFE为平行四边形,从而得到EM∥FN,结合线面平行的判定定理,证出EM∥平面ADF;(2)取AB中点G,连接FG,DG,可得∠FDG为直线DF和平面ABCD所成角,从而可求直线DF和平面ABCD所成角的正切值;(3)求出平面ADF、平面EBAF的一个法向量,利用向量的夹角公式,可求二面角D﹣AF﹣B的大小.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


科目:高中数学 来源: 题型:
【题目】先将函数y=f(x)的图象向左平移 ![]() 个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)若函数y=g(x)与y=f(x)的图象关于点M( ![]() ,2)对称,求函数y=g(x)在[0,
,2)对称,求函数y=g(x)在[0, ![]() ]上的最小值和最大值.
]上的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 和抛物线
和抛物线![]() :
: ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)已知直线![]() 和圆
和圆![]() 相切,与抛物线
相切,与抛物线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过抛物线![]() 上一点
上一点![]() 作两直线
作两直线![]() 和圆
和圆![]() 相切,且分别交抛物线
相切,且分别交抛物线![]() 于
于![]() 两点,若直线
两点,若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: 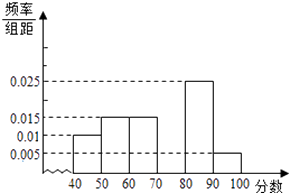
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣ ![]() =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2 ![]() ,求满足条件的实数a的取值.
,求满足条件的实数a的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一直线l过直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为 ![]() 的圆C相切,求圆C的标准方程.
的圆C相切,求圆C的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点. 
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,AD=1,CD=2,AC= ![]() .
. 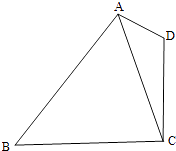
(Ⅰ)求cos∠CAD的值;
(Ⅱ)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设向量 ![]() =(a,
=(a, ![]() ),
), ![]() =(cosC,c﹣2b),且
=(cosC,c﹣2b),且 ![]() ⊥
⊥ ![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=1,求△ABC的周长l的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com