练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，已知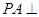矩形ABCD所在平面，M、N分别是AB、PC的中点。

    （1）求证：平面PAD；

    （2）求证：

     

    【答案】

     

    （1）证明略

    （2）证明略

    【解析】（1）取PD的中点E，连接AE、EN，则由于EN与AM平行且相等，

    故AMNE为平行四边形，所以MN//AE

    因为平面PAD，平面PAD，所以MN//平面PAD

    （2）因为矩形ABCD所在平面，所以

    又，所以平面PAD

    所以，即。又CD//AB，

    所以

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图所示，已知在矩形ABCD中，
    AD
    =4
    		3
    ，设
    AB
    =a，
    BC
    =b，
    BD
    =c    ，试求|
    a
    +
    b
    +
    c
    |．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，已知矩形ABCD中，AB=
    		2
    ，AD=1，将△ABD沿BD折起，使点A在平面BCD内的射影落在DC上．
    （1）求证：平面ADC⊥平面BCD；
    （2）求点C到平面ABD的距离；
    （3）若E为BD中点，求二面角B-AD-C的大小．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：047

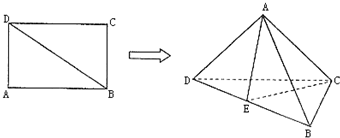
    如图所示，已知矩形ABCD中，AB＝1，BC＝a(a＞0)，PA⊥面ABCD．

    (1)问BC边上是否存在点Q，使得PQ⊥QD，并说明理由．

    (2)若PA＝1，且BC边上有且只有一点Q，使得PQ⊥QD．求这时二面角Q－PD－A的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

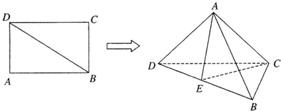    如图所示，已知矩形ABCD中，AB=数学公式，AD=1，将△ABD沿BD折起，使点A在平面BCD内的射影落在DC上．
    （1）求证：平面ADC⊥平面BCD；
    （2）求点C到平面ABD的距离；
    （3）若E为BD中点，求二面角B-AD-C的大小．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年四川省雅安市中学高二（下）期中数学试卷（解析版） 题型：解答题

    如图所示，已知矩形ABCD中，AB=，AD=1，将△ABD沿BD折起，使点A在平面BCD内的射影落在DC上．
    （1）求证：平面ADC⊥平面BCD；
    （2）求点C到平面ABD的距离；
    （3）若E为BD中点，求二面角B-AD-C的大小．

    查看答案和解析>>

    同步练习册答案