
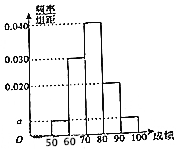
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
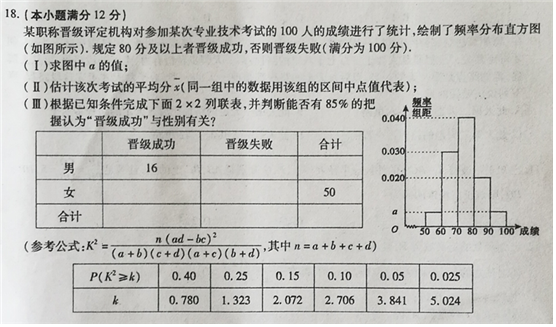
分析 (Ⅰ)由频率和为1,列方程求出a的值;
(Ⅱ)利用直方图中各小组中点乘以对应的频率,求和得平均分;
(Ⅲ)根据题意填写,计算观测值K2,对照临界值得出结论.
解答 解:(Ⅰ)由频率分布直方图各小长方形面积总和为1,得
(2a+0.020+0.030+0.040)×10=1,
解得a=0.005;
(Ⅱ)由频率分布直方图知各小组依次是
[50,60),[60,70),[70,80),[80,90),[90,100],
其中点分别为55,65,75,85,95,
对应的频率分别为0.05,0.30,0.40,0.20,0.05,
计算平均分为
$\overline{x}$=55×0.05+65×0.3+75×0.4+85×0.2+95×0.05=74(分);
(Ⅲ)由频率分布直方图值,晋级成功的频率为0.2+0.05=0.25,
故晋级成功的人数为100×0.25=25,
填写2×2列联表如下,
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | 34 | 50 |
| 女 | 9 | 41 | 50 |
| 合计 | 25 | 75 | 100 |
点评 本题考查了频率分布直方图与独立性检验的应用问题,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
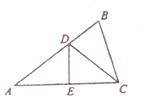 如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.
如图,设△ABC的三个内角A,B,C对应的三条边分别为a,b,c,且角A,B,C成等差数列,a=2,线段AC的垂直平分线分别交线段AB,AC于D,E两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,-1] | B. | (-3,-1] | C. | (-3,-1) | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ca>cb | B. | ac<bc | C. | $\frac{a}{a-c}>\frac{b}{b-c}$ | D. | logac>logbc |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com