
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)若曲线![]() 在点
在点![]() 处切线的斜率为3,且
处切线的斜率为3,且![]() 对任意
对任意![]() 都成立,求整数
都成立,求整数![]() 的最大值.
的最大值.
【答案】(Ⅰ) 极小值![]() ;(Ⅱ)4.
;(Ⅱ)4.
【解析】
试题分析:(Ⅰ)求出导数![]() ,令
,令![]() ,求出根,讨论这些根的两边
,求出根,讨论这些根的两边![]() 的符号,可得极值;(Ⅱ)由导数的几何意义可求得参数
的符号,可得极值;(Ⅱ)由导数的几何意义可求得参数![]() ,这样且
,这样且![]() 对任意
对任意![]() 恒成立,可化为
恒成立,可化为![]() 在
在![]() 上恒成立,这样我们只要求函数
上恒成立,这样我们只要求函数![]() 的最小值即可,当然题目要求整数
的最小值即可,当然题目要求整数![]() 的最大值,故可求最小值的范围,为了讨论
的最大值,故可求最小值的范围,为了讨论![]() 的正负,可能还要对
的正负,可能还要对![]() (或其中部分式子)再求导,通过研究
(或其中部分式子)再求导,通过研究![]() (或其中部分式子)的导数,一步步研究得出结论.
(或其中部分式子)的导数,一步步研究得出结论.
试题解析:(Ⅰ) ![]() 时,
时,![]()
∴![]() ∴
∴![]()
当x变化时,![]() 与
与![]() 变化如下表:
变化如下表:
X |
|
|
|
| - | 0 | + |
| 递减 | 极小值 | 递增 |
∴当![]() 时,
时,![]() 有极小值
有极小值![]() .
.
(Ⅱ)易求得![]() 故问题化为
故问题化为![]() 在
在![]() 上恒成立
上恒成立
令![]() ,则
,则![]()
又令![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 递增,
递增,
又∵![]()
∴![]() 在
在![]() 上有唯一零点,设为
上有唯一零点,设为![]() ,则
,则![]()
且![]() ①
①
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
∴![]()
![]() ,将①代入有
,将①代入有
![]()
所以![]() 所以整数b的最大值为4.
所以整数b的最大值为4.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线 ![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)直线![]() 过
过![]() 且与曲线
且与曲线![]() 相切,求直线
相切,求直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 与点
与点![]() 关于
关于![]() 轴对称,求曲线
轴对称,求曲线![]() 上的点到点
上的点到点![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:
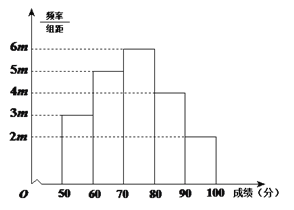
(Ⅰ)求频率分布直方图中![]() 的值;
的值;
(Ⅱ)分别求出成绩落在![]() 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在![]() 的学生中任选2人,求所选学生的成绩都落在
的学生中任选2人,求所选学生的成绩都落在![]() 中的概率
中的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有5个形状大小完全相同的球,其中有2个红球,3个白球.
(1)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(2)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地为制定初中七、八、九年级学生校服的生产计划,有关部门准备对180名初中男生的身高作调查.
(1)为了达到估计该地初中三个年级男生身高分布的目的,你认为采用怎样的调查方案比较合理?
(2)表中的数据是使用了某种调查方法获得的:七、八、九年级180名男生身高:
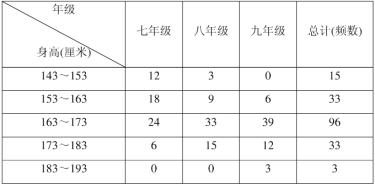
注:表中每组可含最低值,不含最高值.
根据表中的数据,请你给校服生产厂家指定一份生产计划思路.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
资金 | 每台产品所需资金(百元) | 月资金供应量 (百元) | |
空调机 | 洗衣机 | ||
成本 | 30 | 20 | 300 |
劳动力(工资) | 5 | 10 | 110 |
每台产品利润 | 6 | 8 | |
试问:怎样确定两种货物的月供应量,才能使总利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 内有一点
内有一点![]() ,过点
,过点![]() 作直线
作直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(1)当![]() 经过圆心
经过圆心![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当弦![]() 被点
被点![]() 平分时,写出直线
平分时,写出直线![]() 的方程;
的方程;
(3)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求弦
时,求弦![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com