练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】两个非零向量 、 不共线．
    （1）若 = + ， =2 +8 ， =3（ ﹣ ），求证：A、B、D三点共线；
    （2）求实数k使k + 与2 +k 共线．

    【答案】
    （1）证明∵ = + + = + + = =6 ，

    ∴A、B、D三点共线．


    （2）解：∵k + 与2 +k 共线．

    ∴存在实数λ使得k + =λ（2 +k ）．

    ∴（k﹣2λ） +（1﹣λk） = ，

    ∴ ，解得k=± ．

    ∴k=±


    【解析】（1）由 = + + =6 ，即可A、B、D三点共线．（2）由于k + 与2 +k 共线．存在实数λ使得k + =λ（2 +k ）．利用向量基本定理即可得出．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知{an}是一个等差数列，且a2=1，a5=﹣5．
    （1）求{an}的通项an；
    （2）求{an}前n项和Sn的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前n项和， 是等差数列，且.

    （Ⅰ）求数列的通项公式；

    （Ⅱ）令.求数列的前n项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项不为零的数列的前项和为，且， ， ．

    （1）若成等比数列，求实数的值；

    （2）若成等差数列，

    ①求数列的通项公式；

    ②在与间插入个正数，共同组成公比为的等比数列，若不等式对任意的恒成立，求实数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱柱ABCD﹣A1B1C1D1中，底面ABCD是梯形，AD∥BC，侧面ABB1A1为菱形，∠DAB=∠DAA1 ．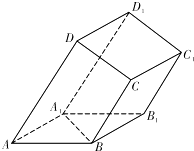
    （Ⅰ）求证：A1B⊥BC；
    （Ⅱ）若AD=AB=3BC，∠A1AB=60°，点D在平面ABB1A1上的射影恰为线段A1B的中点，求平面DCC1D1与平面ABB1A1所成锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（sinx+cosx）2+2cos2x﹣2．
    （1）求函数f（x）的最小正周期及单调递增区间；
    （2）当x∈[ ， ]时，求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= x3+ax2+bx+ （a，b是实数），且f′（2）=0，f（﹣1）=0．
    （1）求实数a，b的值；
    （2）当x∈[﹣1，t]时，求f（x）的最大值g（t）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是根据某班50名同学在某次数学测验中的成绩（百分制）绘制的概率分布直方图，其中成绩分组区间为：[40，50），[50，60），…，[80，90），[90，100]．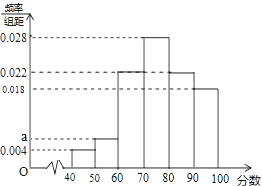

    （1）求图中a的值；
    （2）计算该班本次的数学测验成绩不低于80分的学生的人数；
    （3）根据频率分布直方图，估计该班本次数学测验成绩的平均数与中位数（要求中位数的估计值精确到0.1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学在开学季准备销售一种盒饭进行试创业，在一个开学季内，每售出1盒该盒饭获利润10元，未售出的产品，每盒亏损5元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了150盒该产品，以（单位：盒，）表示这个开学季内的市场需求量，（单位：元）表示这个开学季内经销该产品的利润．

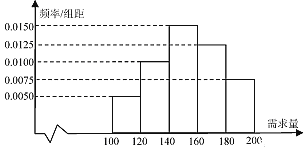
    （Ⅰ）根据直方图估计这个开学季内市场需求量的平均数和众数；

    （Ⅱ）将表示为的函数；

    （Ⅲ）根据频率分布直方图估计利润不少于1350元的概率．

    查看答案和解析>>

    同步练习册答案