
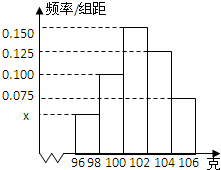
 某公司对工厂A的一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].
某公司对工厂A的一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].
|
| 3 |
| 4 |
| 1 |
| 4 |
| ξ | 66 | 42 | ||||
| P |
|
|
| 3 |
| 4 |
| 1 |
| 4 |


科目:高中数学 来源: 题型:
(本小题满分12分)某公司对工厂A的一批产品进行了抽样检测。右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[10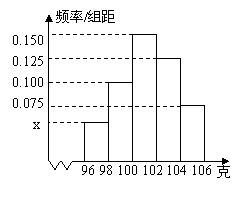 4,106]。
4,106]。
(1)求图中x的值;
(2)若将频率视为概率,从这批产品中有放回地随机抽取3件,求至多有2件产品的净重在![]() 的概率;
的概率;
(3)经过考察后,该公司决定在2011年年初投资到工厂A50万元,到年底可能获利![]() ,也可能亏损
,也可能亏损![]() ,且这两种情况发生的概率分别为合格产品和不合格产品的概率(若产品净重在
,且这两种情况发生的概率分别为合格产品和不合格产品的概率(若产品净重在![]() 为合格产品,其余为不合格产品)。设2011年底公司的投资总资产(本金+利润)为
为合格产品,其余为不合格产品)。设2011年底公司的投资总资产(本金+利润)为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源:2011年广东省佛山市顺德区高考热身数学试卷(理科)(解析版) 题型:解答题
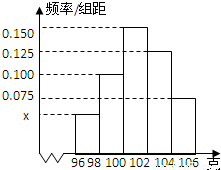
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com