
【题目】已知椭圆C过点![]() ,两个焦点
,两个焦点![]() .
.
(1)求椭圆C的标准方程;
(2)设直线l交椭圆C于A,B两点,且|AB|=6,求△AOB面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由已知可设椭圆方程为![]() (a>b>0),且c
(a>b>0),且c![]() ,再由椭圆定义求得a,结合隐含条件求得b,则椭圆方程可求;
,再由椭圆定义求得a,结合隐含条件求得b,则椭圆方程可求;
(2)当直线AB的斜率不存在时,设直线方程为x=m,由弦长求得m,可得三角形AOB的面积;当直线AB的斜率存在时,设直线方程为y=kx+m,联立直线方程与椭圆方程,结合根与系数的关系及弦长可得m与k的关系,再由点到直线的距离公式求出原点O到AB的距离,代入三角形面积公式,化简后利用二次函数求最值,则答案可求.
解:(1)由题意,设椭圆方程为![]() (a>b>0),
(a>b>0),
且c![]() ,2a
,2a![]() 12,
12,
则a=6,∴b2=a2﹣c2=12.
∴椭圆C的标准方程为![]() ;
;
(2)当直线AB的斜率不存在时,设直线方程为x=m,
得|AB|![]() ,
,
由|AB|![]() 6,解得m=±3,
6,解得m=±3,
此时![]() ;
;
当直线AB的斜率存在时,设直线方程为y=kx+m,
联立 ,得(3k2+1)x2+6kmx+3m2﹣36=0.
,得(3k2+1)x2+6kmx+3m2﹣36=0.
△=36k2m2﹣4(3k2+1)(3m2﹣36)=432k2﹣12m2+144.
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
则![]() ,
,![]() .
.
由|AB|![]() 6,
6,
整理得:![]() ,原点O到AB的距离d
,原点O到AB的距离d![]() .
.
∴![]()
![]() .
.
当![]() 时,△AOB面积有最大值为
时,△AOB面积有最大值为![]() 9.
9.
综上,△AOB面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“巧值点”,则下列函数中有“巧值点”的是________.
①f(x)=x2;②f(x)=e-x;③f(x)=lnx;④f(x)=tanx;⑤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.
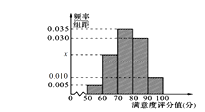
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,ABCD为菱形,∠ABC=60°,△PAB是边长为2的等边三角形,点M为AB的中点,将△PAB沿AB边折起,使平面PAB⊥平面ABCD,连接PC、PD,如图2,
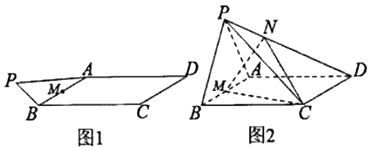
(1)证明:AB⊥PC;
(2)求PD与平面ABCD所成角的正弦值
(3)在线段PD上是否存在点N,使得PB∥平面MC?若存在,请找出N点的位置;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com