
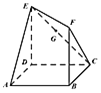
【题目】如图,四边形ABCD是边长为1的正方形,![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,且
平面ABCD,且![]() ,G为线段EC上的动点,则下列结论中正确的是______
,G为线段EC上的动点,则下列结论中正确的是______
![]() ;
;![]() 该几何体外接球的表面积为
该几何体外接球的表面积为![]() ;
;
![]() 若G为EC中点,则
若G为EC中点,则![]() 平面AEF;
平面AEF;
![]() 的最小值为3.
的最小值为3.
【答案】![]()
【解析】
以D为原点,DA所在直线为x轴,DC所在直线为y轴,DE所在直线为z轴,建立空间直角坐标系,分别求得D,A,B,C,F,E的坐标,由![]() ,
,![]() 的坐标表示,可判断
的坐标表示,可判断![]() ;确定球心为矩形BDEF的对角线交点,求得半径,可判断
;确定球心为矩形BDEF的对角线交点,求得半径,可判断![]() ;求得G的坐标,求得平面AEF的法向量,计算可判断
;求得G的坐标,求得平面AEF的法向量,计算可判断![]() ;设出G的坐标,由两点的距离公式,结合二次函数的最值求法,可判断
;设出G的坐标,由两点的距离公式,结合二次函数的最值求法,可判断![]() .
.
以D为原点,DA所在直线为x轴,DC所在直线为y轴,DE所在直线为z轴,
建立空间直角坐标系,

可得![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
即有![]() 1,
1,![]() ,
,![]() 1,
1,![]() ,由
,由![]() ,可得
,可得![]() ,故
,故![]() 正确;
正确;
由球心在过正方形ABCD的中心的垂面上,即为矩形BDEF的对角线的交点,
可得半径为![]() ,即有该几何体外接球的表面积为
,即有该几何体外接球的表面积为![]() ,故
,故![]() 正确;
正确;
若G为EC中点,可得![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,
设平面AEF的法向量为![]() y,
y,![]() ,可得
,可得![]() ,且
,且![]() ,可设
,可设![]() ,可得一个法向量为
,可得一个法向量为![]() ,
,
由![]() ,可得
,可得![]() 则
则![]() 平面AEF,故
平面AEF,故![]() 正确;
正确;
设![]() t,
t,![]() ,
, ,
,
当![]() 时,取得最小值
时,取得最小值![]() ,故
,故![]() 错误.
错误.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】一辆单向行驶的汽车,满载为25人,全程共设14个车站,途中每个车站均可上下乘客,由不同的起点到达不同的终点的乘客应购买不同的车票,在一次单程行驶中,车上最多卖出不同的车票的个数是( )
A.63B.65C.67D.69
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | y | m |
非单车用户 | x | 32 | 70 |
合计 | n | 50 | 100 |
(1)求出列联表中字母x、y、m、n的值;
(2)①从此样本中,对单车用户按年龄采取分层抽样的方法抽出5人进行深入调研,其中不小于40岁的人应抽多少人?
②从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为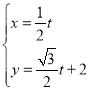 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求直线![]() 被曲线
被曲线![]() 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() ,以
,以![]() 为边在轴上方作一个平行四边形
为边在轴上方作一个平行四边形![]() ,满足
,满足![]() .
.
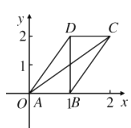
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)将动点![]() 的轨迹方程所表示的曲线
的轨迹方程所表示的曲线![]() 向左平移
向左平移![]() 个单位得曲线,若
个单位得曲线,若![]() 是曲线
是曲线![]() 上的一点,当
上的一点,当 时,记
时,记![]() 为点
为点![]() 到直线
到直线![]() 距离的最大值,求
距离的最大值,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com