
【题目】已知函数f(x)=(x﹣1)ex+ax2(a∈R).
(1)若a=e,求函数f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性.
【答案】(1)3ex﹣y﹣2e=0(2)①当a≥0时, y=f(x)在(﹣∞,0)上为减函数,在(0,+∞)上为增函数;
②当![]() 时y=f(x) 在 (﹣∞,ln(﹣2a)),(0,+∞)上为增函数,在(ln(﹣2a),0)上为减函数;
时y=f(x) 在 (﹣∞,ln(﹣2a)),(0,+∞)上为增函数,在(ln(﹣2a),0)上为减函数;
③若![]() 时,y=f(x)在
时,y=f(x)在![]() 上为单调递增的;
上为单调递增的;
④若![]() 时,y=f(x)在(﹣∞,0),(ln(﹣2a),+∞)上为增函数,在(0,ln(﹣2a)) 上为减函数.
时,y=f(x)在(﹣∞,0),(ln(﹣2a),+∞)上为增函数,在(0,ln(﹣2a)) 上为减函数.
【解析】
(1)由a=e得f(x)=(x﹣1)ex+ex2.再![]() =xex+2ex,分别求得
=xex+2ex,分别求得![]() ,f(1),用点斜式写出切线方程..
,f(1),用点斜式写出切线方程..
(2)根据![]() =x(ex+2a),分a≥0,
=x(ex+2a),分a≥0, ![]() ,
,![]() ,
,![]() 四种情况分类讨论.
四种情况分类讨论.
(1)∵a=e,
∴f(x)=(x﹣1)ex+ex2.
∴![]() =xex+2ex,
=xex+2ex,
∴![]() =3e,f(1)=e.
=3e,f(1)=e.
∴y﹣e=3e(x﹣1),
所以切线方程是3ex﹣y﹣2e=0;
(2)∵![]() =x(ex+2a)
=x(ex+2a)
①若a≥0时,ex+2a>0.
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
所以y=f(x)在(﹣∞,0)上为减函数,在(0,+∞)上为增函数;
②若![]() 时,ln(﹣2a)<0,
时,ln(﹣2a)<0,
当x<ln(﹣2a)或x>0,![]() >0,
>0,
当ln(﹣2a)<x<0时,![]() <0,
<0,
∴y=f(x) 在 (﹣∞,ln(﹣2a)),(0,+∞)上为增函数,在(ln(﹣2a),0)上为减函数;
③若![]() 时,ln(﹣2a)=0,
时,ln(﹣2a)=0,![]() >0成立,所以y=f(x)在
>0成立,所以y=f(x)在![]() 上为单调递增的;
上为单调递增的;
④若![]() 时,ln(﹣2a)>0,
时,ln(﹣2a)>0,
当x>ln(﹣2a)或x<0时,![]() >0,
>0,
当0<x<ln(﹣2a)时,![]() <0,
<0,
∴y=f(x)在(﹣∞,0),(ln(﹣2a),+∞)上为增函数,在(0,ln(﹣2a)) 上为减函数.
综上:①若a≥0时, y=f(x)在(﹣∞,0)上为减函数,在(0,+∞)上为增函数;
②若![]() 时, y=f(x) 在 (﹣∞,ln(﹣2a)),(0,+∞)上为增函数,在(ln(﹣2a),0)上为减函数;
时, y=f(x) 在 (﹣∞,ln(﹣2a)),(0,+∞)上为增函数,在(ln(﹣2a),0)上为减函数;
③若![]() 时, y=f(x)在
时, y=f(x)在![]() 上为单调递增的;
上为单调递增的;
④若![]() 时,y=f(x)在(﹣∞,0),(ln(﹣2a),+∞)上为增函数,在(0,ln(﹣2a)) 上为减函数.
时,y=f(x)在(﹣∞,0),(ln(﹣2a),+∞)上为增函数,在(0,ln(﹣2a)) 上为减函数.


科目:高中数学 来源: 题型:
【题目】如图①,利用斜二侧画法得到水平放置的![]() 的直观图
的直观图![]() ,其中
,其中![]() 轴,
轴,![]() 轴.若
轴.若![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,记
,记![]() ,执行如图②的框图,则输出
,执行如图②的框图,则输出![]() 的值
的值
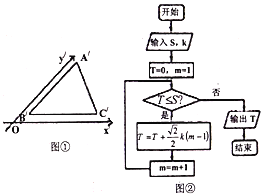
A. 12B. 10C. 9D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是函数f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数![]() ,请你根据上面探究结果,计算f(
,请你根据上面探究结果,计算f(![]() )+f(
)+f(![]() )+f(
)+f(![]() )+……+f(
)+……+f(![]() )=_____.
)=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ,g(x)
,g(x)![]() 1.
1.
(1)若f(a)=2,求实数a的值;
(2)判断f(x)的单调性,并证明;
(3)设函数h(x)=g(x)![]() (x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
(x>0),若h(2t)+mh(t)+4>0对任意的正实数t恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,△PAD是一个正三角形,若平面PAD⊥平面ABCD,则该四棱锥的外接球的表面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 恰好在线段
恰好在线段![]() 的垂直平分线上,以
的垂直平分线上,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 底面
底面![]() ,如图2所示,
,如图2所示,![]() 是线段
是线段![]() 的中点.
的中点.
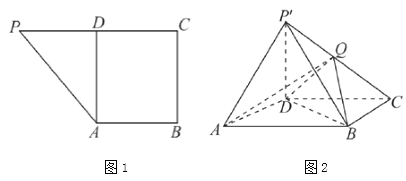
(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为1,求
的体积为1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积的经验公式为:![]() .弧田(如图1阴影部分)由圆弧和其所对弦围成,弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.类比弧田面积公式得到球缺(如图 2)近似体积公式:
.弧田(如图1阴影部分)由圆弧和其所对弦围成,弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.类比弧田面积公式得到球缺(如图 2)近似体积公式:![]() 圆面积
圆面积![]() 矢
矢![]() .球缺是指一个球被平面截下的一部分,厦门嘉庚体育馆近似球缺结构(如图3),若该体育馆占地面积约为18000
.球缺是指一个球被平面截下的一部分,厦门嘉庚体育馆近似球缺结构(如图3),若该体育馆占地面积约为18000![]() ,建筑容积约为340000
,建筑容积约为340000![]() ,估计体育馆建筑高度(单位:
,估计体育馆建筑高度(单位:![]() )所在区间为( )
)所在区间为( )
参考数据: ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.



A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com