
【题目】已知函数![]() .
.
(1)若![]() ,求函数的单调区间;
,求函数的单调区间;
(2)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
试题分析:(1)求导![]() ,考虑
,考虑![]() .分类讨论
.分类讨论![]() 的符号,即可得函数的单调性;(2)
的符号,即可得函数的单调性;(2)![]() ,令
,令![]() , 由
, 由![]() ,可知
,可知![]() 在
在![]() 有且仅有一个零点,设为
有且仅有一个零点,设为![]() ,利用
,利用![]() 讨论函数
讨论函数![]() 的单调性并求出最小值,即可得出结论.
的单调性并求出最小值,即可得出结论.
试题解析:
(1)函数的定义域为![]() . 若
. 若![]() ,
,
则![]() ,
,
考虑![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,故
,故![]() 恒成立,
恒成立,
此时![]() 在
在![]() 单调递增.
单调递增.
当![]() 时,
时,![]() ,即方程
,即方程![]() 有2个根
有2个根
由根与系数之间的关系可得![]() ,
,
即![]() ,
,
故![]() 时,
时,![]() ,
,
此时![]() 在
在![]() 单调递增.
单调递增.
当![]() 时,
时,![]() ,
,
即方程![]() 有2个根
有2个根![]() ,
,
由根与系数之间的关系可得![]() ,
,
即![]() ,
,
当![]() 或
或![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减.
单调递减.
此时![]() 在
在![]() 单调递增.
单调递增.
综上![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() .
.
当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,
,
![]() 的单调减区间为
的单调减区间为![]() .
.
(2) 若![]() ,则
,则![]() ,
,
则令![]() , 由
, 由![]() ,可知
,可知![]() 在
在![]() 有且仅有一个零点,设为
有且仅有一个零点,设为![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,故
,故![]() 在
在![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,即
,即![]() ,故
,故![]() 在
在![]() 单调递增,
单调递增,
所以![]()
又![]() 即
即![]()
依题意![]() ,即
,即![]() ,
,
易知![]() 在
在![]() 单调递增,
单调递增,
且![]() ,故
,故![]() , 又
, 又![]() ,即
,即![]() ,
,
易知![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】己知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,则直线
,则直线![]() 称为抛物线
称为抛物线![]() 的伴随直线.
的伴随直线.
(1)求抛物线![]() 的伴随直线的表达式;
的伴随直线的表达式;
(2)已知抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与
,且该抛物线与![]() 轴有两个不同的公共点,求
轴有两个不同的公共点,求![]() 的取值范围.
的取值范围.
(3)已知![]() ,若抛物线
,若抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与线段
,且该抛物线与线段![]() 恰有1个公共点,求
恰有1个公共点,求![]() 的取值范围(直接写出答案即可)
的取值范围(直接写出答案即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
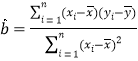
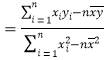 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据不完全统计,某厂的生产原料耗费![]() (单位:百万元)与销售额
(单位:百万元)与销售额![]() (单位:百万元)如下:
(单位:百万元)如下:
| 2 | 4 | 6 | 8 |
| 30 | 40 | 50 | 70 |
变量![]() 、
、![]() 为线性相关关系.
为线性相关关系.
(1)求线性回归方程必过的点;
(2)求线性回归方程;
(3)若实际销售额要求不少于![]() 百万元,则原材料耗费至少要多少百万元。
百万元,则原材料耗费至少要多少百万元。
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:
7327 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地新建一家服装厂,从今年7月份开始投产,并且前4个月的产量分别为![]() 万件、
万件、![]() 万件、
万件、![]() 万件、
万件、![]() 万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:
万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:![]() ,
,![]() ,
,![]() ,
,![]() .你将利用零一种模型去估算以后几个月的产量?
.你将利用零一种模型去估算以后几个月的产量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x) .
.

(1)画出函数f(x)的图象,根据图象直接写出f(x)的值域;
(2)根据图象直接写出满足f(x)≥2的所有x的集合;
(3)若f(x)的递减区间为(﹣∞,a),递增区间为(b,+∞),直接写出a的最大值,b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E、F分别是PC、AD中点,
(1)求证:DE//平面PFB;
(2)求PB与面PCD所成角的正切值。

查看答案和解析>>
科目:高中数学 来源: 题型:
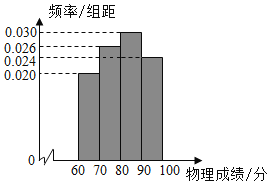
【题目】为了解某校高一1000名学生的物理成绩,随机抽查了部分学生的期中考试成绩,将数据整理后绘制成如图所示的频率分布直方图.
(1)估计该校高一学生物理成绩不低于80分的人数;
(2)若在本次考试中,规定物理成绩在m分以上(包括m分)的为优秀,该校学生物理成绩的优秀率大约为18%,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com