Question

甲、乙两人共同投掷一枚硬币，规定硬币正面朝上甲得1分，否则乙得1分，先积3分者获胜，并结束游戏．
①求在前3次投掷中甲得2分，乙得1分的概率．
②设ξ表示到游戏结束时乙的得分，求ξ的分布列以及期望．

Answer 1

分析：（1）由题意知本题是一个古典概型试验发生的事件是掷一枚硬币3次，出现的所有可能情况通过列举共有8种．满足条件的事件是其中甲得（2分），乙得（1分）的情况从8种中看出有以下3种，根据古典概型公式得到结果．
（2）ξ表示到游戏结束时乙的得分，因为共掷三次，所以变量的可能取值是0、1、2、3，结合变量对应的事件，得到概率，写出分布列和期望．

解答：解：（1）由题意知本题是一个古典概型
试验发生的事件是掷一枚硬币3次，出现的所有可能情况共有以下8种．
（正正正）、（正正反）、（正反反）、（反反反）、（正反正）、（反正正）、（反反正）、（反正反）、
其中甲得（2分），乙得（1分）的情况有以下3种，（正正反）、（正反正）、（反正正）
∴所求概率P=

3

8

（2）ξ的所有可能值为：0、1、2、3
P(ξ=0)=

1

2

×

1

2

×

1

2

=

1

8

P(ξ=1)=

C

1 3

×

1

2

×(

1

2

)2×

1

2

=

3

16

，P(ξ=2)=

C

2 4

(

1

2

)2(

1

2

)2

1

2

=

3

16

P(ξ=3)=

1

2

×

1

2

×

1

2

+

C

1 3

1

2

(

1

2

)2

1

2

+

C

2 4

(

1

2

)2(

1

2

)2

1

2

=

1

2

∴ξ的分布列为：

∴Eξ=1×

3

16

+2×

3

16

+3×

1

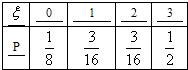
2

=

33

16

点评：考查运用概率知识解决实际问题的能力，注意满足独立重复试验的条件，解题过程中判断概率的类型是难点也是重点，这种题目高考必考，应注意解题的格式．