
【题目】已知命题P:方程x2+mx+1=0有两个不等的实数根,命题q:方程4x2+4(m﹣2)x+1=0无实数根.若p∧q为假,若p∨q为真,求m的取值范围.
【答案】解:P真:△=m2﹣4>0m>2或m<﹣2;
Q真:△=16(m﹣2)2﹣16<0﹣1<m﹣2<11<m<3;
若P∨Q为真,P∧Q为假,则有P真Q假或Q真P假.
当P真Q假时,  m<﹣2或m≥3;
m<﹣2或m≥3;
当P假Q真时, ![]() 1<m≤2;
1<m≤2;
∴满足题意的实数m的取值范围为:m<﹣2或1<m≤2或m≥3
【解析】根据题意,可分别求得P真与Q真时m的范围,再根据复合命题间的关系分P真Q假与P假Q真两类讨论即可求得实数m的取值范围.
【考点精析】认真审题,首先需要了解复合命题的真假(“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真).


科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() ,则不等式f(t﹣1)+f(t)<0的解集为( )
,则不等式f(t﹣1)+f(t)<0的解集为( )
A.(0,1)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,试估计该校学生每周平均体育运动时间超过4小时的概率.
,试估计该校学生每周平均体育运动时间超过4小时的概率.
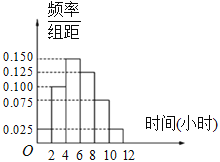
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关?
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
合计 | 300 |
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣2,1)
B.(﹣2,1)
C.(﹣∞,﹣2)∪(1,+∞)
D.(﹣∞,﹣2]∪[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间地面面积为12m2的背面靠墙的矩形小房子,由于地理位置的限制,房子侧面的长度x不得超过am.房屋正面的造价为400元/m2 , 房屋侧面的造价为150元/m2 , 屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.当侧面的长度为多少时,总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)两个共轭复数的差是纯虚数;(2)两个共轭复数的和不一定是实数;(3)若复数a+bi(a,b∈R)是某一元二次方程的根,则a﹣bi是也一定是这个方程的根;(4)若z为虚数,则z的平方根为虚数,
其中正确的个数为( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() 且an+1=an﹣an2(n∈N*)
且an+1=an﹣an2(n∈N*)
(1)证明:1< ![]() ≤2(n∈N*);
≤2(n∈N*);
(2)设数列{an2}的前n项和为Sn , 证明 ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com